experimental probability math is fun definition

Experimental Probability

Experimental probability: introduction, experimental probability: definition, experimental probability formula, solved examples, practice problems, frequently asked questions.

In mathematics, probability refers to the chance of occurrence of a specific event. Probability can be measured on a scale from 0 to 1. The probability is 0 for an impossible event. The probability is 1 if the occurrence of the event is certain.

There are two approaches to study probability: experimental and theoretical. 

Suppose you and your friend toss a coin to decide who gets the first turn to ride a new bicycle. You choose “heads” and your friend chooses “tails.” 

Can you guess who will win? No! You have $\frac{1}{2}$ a chance of winning and so does your friend. This is theoretical since you are predicting the outcome based on what is expected to happen and not on the basis of outcomes of an experiment.

So, what is the experimental probability? Experimental probability is calculated by repeating an experiment and observing the outcomes. Let’s understand this a little better.

Recommended Games

Experimental probability, or empirical probability, is the probability calculated by performing actual experiments and gathering or recording the necessary information. How would you define an experiment? The math definition of an experiment is “a process or procedure that can be repeated and that has a set of well-defined possible results or outcomes.”

Consider the same example. Suppose you flip the coin 50 times to see whether you get heads or tails, and you record the outcomes. Suppose you get heads 20 times and tails 30 times. Then the probability calculated using these outcomes is experimental probability. Here, t he experimental meaning is connected with such experiments used to determine the probability of an event.

Now that you know the meaning of experimental probability, let’s understand its formula.

Experimental Probability for an Event A can be calculated as follows:

P(E) $= \frac{Number of occurance of the event A}{Total number of trials}$

Let’s understand this with the help of the last example. 

A coin is flipped a total of 50 times. Heads appeared 20 times. Now, what is the experimental probability of getting heads?

E xperimental probability of getting heads $= \frac{Number of occurrences}{Total number of trials}$

P (Heads) $= \frac{20}{50} = \frac{2}{5}$

P (Tails) $= \frac{30}{50} = \frac{3}{5}$

Experimental Probability vs. Theoretical Probability

Theoretical probability expresses what is expected. On the other hand, experimental probability explains how frequently an event occurred in an experiment.

If you roll a die, the theoretical probability of getting any particular number, say 3, is $\frac{1}{6}$. 

However, if you roll the die 100 times and record how many times 3 appears on top, say 65 times, then the experimental probability of getting 3 is $\frac{65}{100}$.

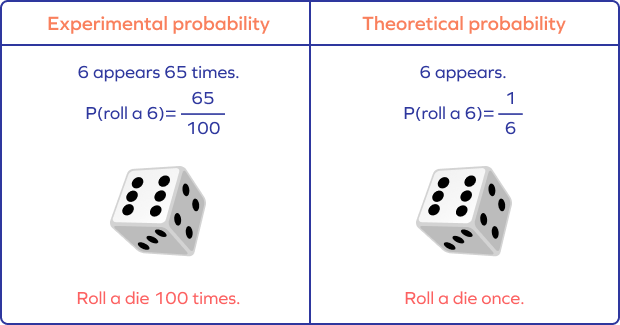
Theoretical probability for Event A can be calculated as follows:

P(A) $= \frac{Number of outcomes favorable to Event A}{Number of possible outcomes}$

In the example of flipping a coin, the theoretical probability of the occurrence of heads (or tails) on tossing a coin is

P(H) $= \frac{1}{2}$ and  P(T) $= \frac{1}{2}$ (since possible outcomes are $2 -$ head or tail)

Experimental Probability: Examples

Let’s take a look at some of the examples of experimental probability .

Example 1: Ben tried to toss a ping-pong ball in a cup using 10 trials, out of which he succeeded 4 times. 

P(win) $= \frac{Number of success}{Number of trials}$

             $= \frac{4}{10}$

             $= \frac{2}{5}$

Example 2: Two students are playing a game of die. They want to know how many times they land on 2 on the dice if the die is rolled 20 times in a row. 

The experimental probability of rolling a 2 

$= \frac{Number of times 2 appeared}{Number of trials}$

$= \frac{5}{20}$

$= \frac{1}{4}$

1. Probability of an event always lies between 0 and 1.

2. You can also express the probability as a decimal and a percentage.

Experimental probability is a probability that is determined by the results of a series of experiments. Learn more such interesting concepts at SplashLearn .

1. Leo tosses a coin 25 times and observes that the “head” appears 10 times. What is the experimental probability of getting a head?

 P(Head) $= \frac{Number of times heads appeared}{Total number of trials}$

               $= \frac{10}{25}$

               $= \frac{2}{5}$

               $= 0.4$

2. The number of cakes a baker makes per day in a week is given as 7, 8, 6, 10, 2, 8, 3. What is the probability that the baker makes less than 6 cakes the next day?

Solution: 

Number of cakes baked each day in a week $= 7, 8, 6, 10, 2, 8, 3$

Out of 7 days, there were 2 days (highlighted in bold) on which the baker made less than 6 cookies.

P$(< 6 $cookies$) = \frac{2}{7}$

3. The chart below shows the number of times a number was shown on the face of a tossed die. What was the probability of getting a 3 in this experiment?

Number of times 3 showed $= 7$

Number of tosses $= 30$

P(3) $= \frac{7}{30}$

4. John kicked a ball 20 times. He kicked 16 field goals and missed 4 times . What is the experimental probability that John will kick a field goal during the game?

Solution:  

John succeeded in kicking 16 field goals. He attempted to kick a field goal 20 times. 

So, the number of trials $= 20$

John’s experimental probability of kicking a field goal $= \frac{Successful outcomes} {Trials attempted} = \frac{16}{20}$ 

$= \frac{4}{5}$

$= 0.8$ or $80%$

5. James recorded the color of bikes crossing his street. Of the 500 bikes, 10 were custom colors, 100 were white, 50 were red, 120 were black, 100 were silver, 60 were blue, and 60 were gray. What is the probability that the car crossing his street is white?

Number of white bikes $= 100$ 

Total number of bikes $= 500$

P(white bike) $=  \frac{100}{500} = \frac{1}{5}$

Attend this quiz & Test your knowledge.

In a class, a student is chosen randomly in five trials to participate in 5 different events. Out of chosen students, 3 were girls and 2 were boys. What is the experimental probability of choosing a boy in the next event?

A manufacturer makes 1000 tablets every month. after inspecting 100 tablets, the manufacturer found that 30 tablets were defective. what is the probability that you will buy a defective tablet, the 3 coins are tossed 1000 times simultaneously and we get three tails $= 160$, two tails $= 260$, one tail $= 320$, no tails $= 260$. what is the probability of occurrence of two tails, the table below shows the colors of shirts sold in a clothing store on a particular day and their respective frequencies. use the table to answer the questions that follow. what is the probability of selling a blue shirt.

Jason leaves for work at the same time each day. Over a period of 327 working days, on his way to work, he had to wait for a train at the railway crossing for 68 days. What is the experimental probability that Jason has to wait for a train on his way to work?

What is the importance of experimental probability?

Experimental probability is widely used in research and experiments in various fields, such as medicine, social sciences, investing, and weather forecasting.

Is experimental probability always accurate?

Predictions based on experimental probability are less reliable than those based on theoretical probability.

Can experimental probability change every time the experiment is performed?

Since the experimental probability is based on the actual results of an experiment, it can change when the results of an experiment change.

What is theoretical probability?

The theoretical probability is calculated by finding the ratio of the number of favorable outcomes to the total number of probable outcomes.

RELATED POSTS

• Length Conversion – Metric and Customary System, Examples
• How Many Weeks Are There in a Month? Definition with Examples
• Analog Clock – Definition, Clock Face, Clock Hands, Examples, Facts
• Slope of Parallel Line: Formula, Derivation, Example
• Milliliter – Definition with Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Prob. distribution

Experimental prob.

Experimental probability

Here you will learn about experimental probability, including using the relative frequency and finding the probability distribution.

Students will first learn about experimental probability as part of statistics and probability in 7 th grade.

What is experimental probability?

Experimental probability is the probability of an event happening based on an experiment or observation.

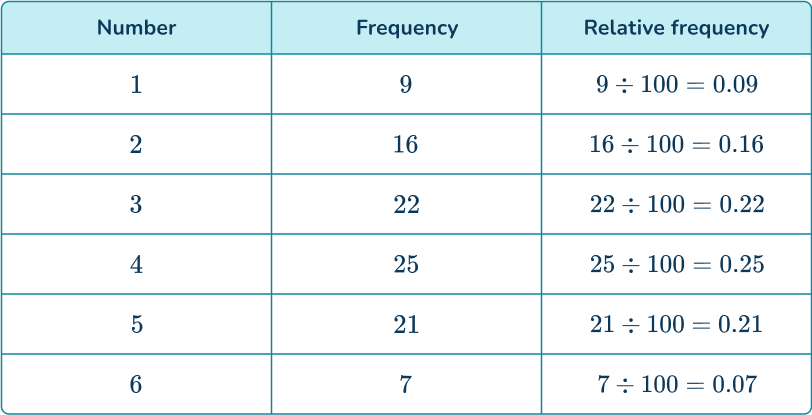
To calculate the experimental probability of an event, you calculate the relative frequency of the event.

Relative frequency =\cfrac{\text{frequency of event occurring}}{\text{total number of trials of the experiment}}

You can also express this as R=\cfrac{f}{n} where R is the relative frequency, f is the frequency of the event occurring, and n is the total number of trials of the experiment.

If you find the relative frequency for all possible events from the experiment, you can write the probability distribution for that experiment.

The relative frequency, experimental probability, and empirical probability are the same thing and are calculated using the data from random experiments. They also have a key use in real-life problem-solving.

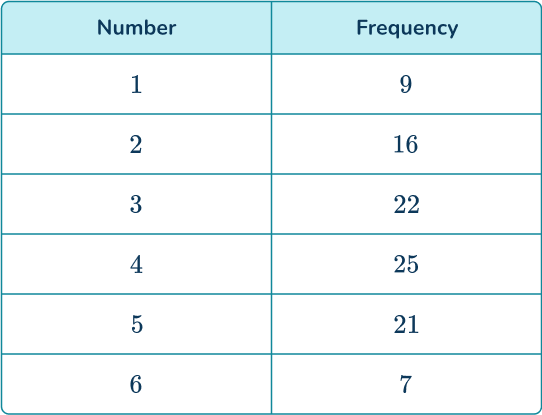
For example, Jo made a four-sided spinner out of cardboard and a pencil.

She spun the spinner 50 times. The table shows the number of times the spinner landed on each of the numbers 1 to 4. The final column shows the relative frequency.

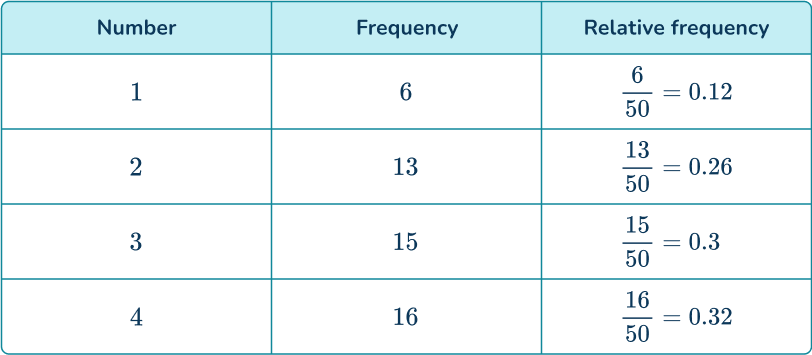
The relative frequencies of all possible events will add up to 1.

This is because the events are mutually exclusive.

See also: Mutually exclusive events

[FREE] Probability Check for Understanding Quiz (Grade 7 to 12)

Use this quiz to check your grade 7 to 12 students’ understanding of probability. 15+ questions with answers covering a range of 7th to 12th grade probability topics to identify areas of strength and support!

Experimental probability vs theoretical probability

You can see that the relative frequencies are not equal to the theoretical probabilities you would expect if the spinner was fair.

If the spinner is fair, the more times an experiment is done, the closer the relative frequencies should be to the theoretical probabilities.

In this case, the theoretical probability of each section of the spinner would be 0.25, or \cfrac{1}{4}.

Step-by-step guide: Theoretical probability

Common Core State Standards

How does this relate to 7 th grade math?

• Grade 7 – Statistics & Probability (7.SP.C.5) Understand that the probability of a chance event is a number between 0 and 1 that expresses the likelihood of the event occurring. Larger numbers indicate greater likelihood. A probability near 0 indicates an unlikely event, a probability around \cfrac{1}{2} indicates an event that is neither unlikely nor likely, and a probability near 1 indicates a likely event.

How to find an experimental probability distribution

In order to calculate an experimental probability distribution:

Draw a table showing the frequency of each outcome in the experiment.

Determine the total number of trials.

Write the experimental probability (relative frequency) of the required outcome(s).

Experimental probability examples

Example 1: finding an experimental probability distribution.

A 3- sided spinner numbered 1, \, 2, and 3 is spun and the results are recorded.

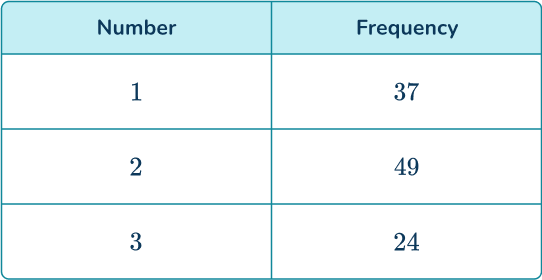
Find the probability distribution for the 3- sided spinner from these experimental results.

A table of results has already been provided. You can add an extra column for the relative frequencies.

2 Determine the total number of trials.

3 Write the experimental probability (relative frequency) of the required outcome(s).

Divide each frequency by 110 to find the relative frequencies.

Example 2: finding an experimental probability distribution

A normal 6- sided die is rolled 50 times. A tally chart was used to record the results.

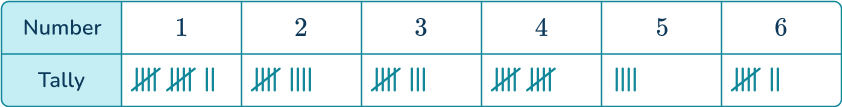
Determine the probability distribution for the 6- sided die. Give your answers as decimals.

Use the tally chart to find the frequencies and add a row for the relative frequencies.

The question stated that the experiment had 50 trials. You can also check that the frequencies add up to 50.

Divide each frequency by 50 to find the relative frequencies.

Example 3: using an experimental probability distribution

A student made a biased die and wanted to find its probability distribution for use in a game. They rolled the die 100 times and recorded the results.

By calculating the probability distribution for the die, determine the probability of the die landing on a 3 or a 4.

The die was rolled 100 times.

You can find the probability of rolling a 3 or a 4 by adding the relative frequencies for those numbers.

P(3\text{ or }4)=0.22+0.25=0.47

Note: P(\text{Event }A) means the probability of event A occurring.

Alternatively, it is only necessary to calculate the relative frequencies for the desired events but by calculating all of the relative frequencies and finding the sum of these values, your solution should equal 1.

The frequency of rolling a 3 or a 4 is 22+25=47.

As the total frequency is 100, the relative frequency is \cfrac{47}{100}=0.47.

Example 4: calculating the relative frequency without a known frequency of outcomes

A research study asked 1,200 people how they commute to work. 640 travel by car, 174 use the bus, and the rest walk. Determine the relative frequency of someone walking to work.

Writing the known information into a table, you have

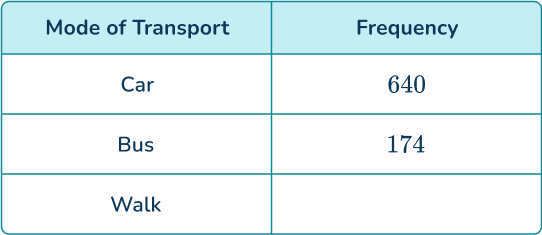
You currently do not know the frequency of people who walk to work. You can calculate this as you know the total frequency.

The number of people who walk to work is equal to

1200-(640+174)=386.

You now have the full table,

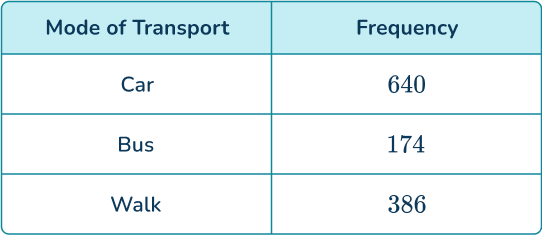
The total frequency is 1,200.

Divide each frequency by the total number of people (1,200), you have

The relative frequency of someone walking to work is 0.3216.

How to find a frequency using an experimental probability

In order to calculate a frequency using an experimental probability:

Determine the experimental probability of the event.

Multiply the total frequency by the experimental probability.

Example 5: calculating a frequency

A dice was rolled 300 times. The experimental probability of rolling an even number is \cfrac{27}{50}. How many times was an even number rolled?

The experimental probability is \cfrac{27}{50}.

An even number was rolled 162 times.

Example 6: calculating a frequency

A bag contains different colored counters. A counter is selected at random and replaced back into the bag 240 times. The probability distribution of the experiment is given below.

Determine the total number of times a blue counter was selected.

As the events are mutually exclusive, the sum of the probabilities must be equal to 1.

This means that you can determine the value of x.

1-(0.4+0.25+0.15)=0.2

The experimental probability (relative frequency) of a blue counter is 0.2.

Multiplying the total frequency by 0.2, you have

240 \times 0.2=48

A blue counter was selected 48 times.

Teaching tips for experimental probability

• Relate probability to everyday situations, such as the chance of getting heads or tails when flipping a fair coin, to make the concept more tangible.
• Rather than strictly using worksheets, let students conduct their own experiments, such as rolling dice or drawing marbles from a bag, to collect data and compute probabilities.
• Emphasize that in mathematics, experimental probability is based on actual trials or experiments, as opposed to theoretical probability which is based on possible outcomes.
• Teach students how to record the results of an experiment systematically and use them to calculate probabilities. Use charts or tables to help visualize the data.
• Discuss events that cannot occur, such as rolling a 7 with a single six-sided die. Explain that the probability of impossible events is always 0. This helps students understand the concept of probability in a broader context.

Easy mistakes to make

• Forgetting the differences between theoretical and experimental probability It is common to forget to use the relative frequencies from experiments for probability questions and use the theoretical probabilities instead. For example, they may be asked to find the probability of a die landing on an even number based on an experiment and the student will incorrectly answer it as 0.5.
• Thinking the relative frequency is an integer The relative frequency is the same as the experimental probability. This value is written as a fraction, decimal, or percentage, not an integer.
• Assuming future results will be the same Students might think that if an experiment yields a certain probability on one day, the results will be the same the next day. Explain that while probabilities are consistent over time in theory, each set of trials can have different outcomes due to randomness, and variations can occur from day to day.

Related probability distribution lessons

• Probability distribution
• Expected frequency

Practice experimental probability questions

1. A coin is flipped 80 times and the results are recorded.

Determine the probability distribution of the coin.

As the number of tosses is 80, dividing the frequencies for the number of heads and the number of tails by 80, you have

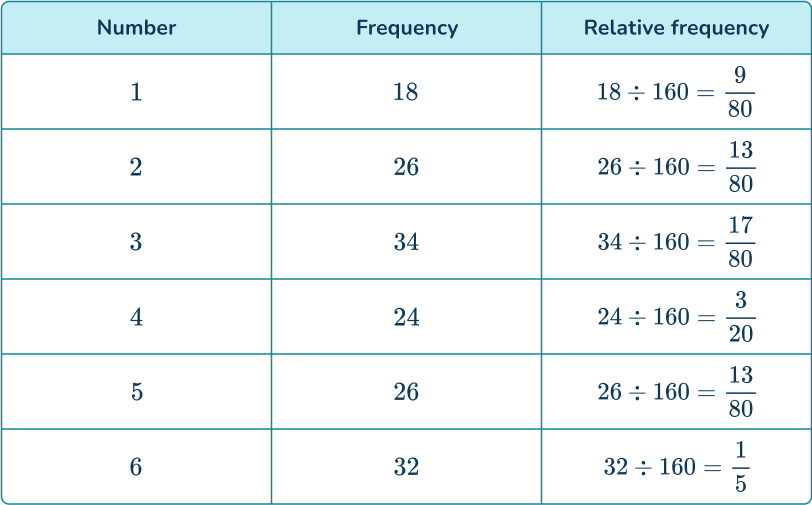
2. A 6- sided die is rolled 160 times and the results are recorded.

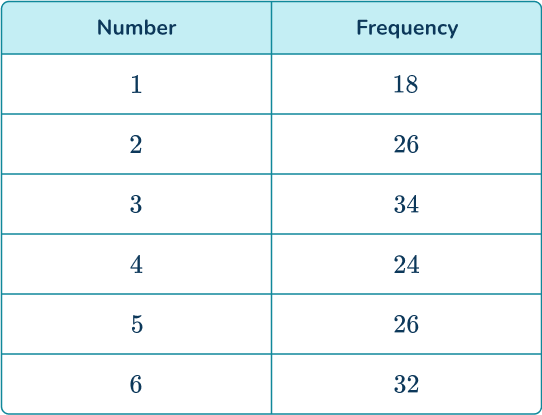
Determine the probability distribution of the die. Write your answers as fractions in their simplest form.

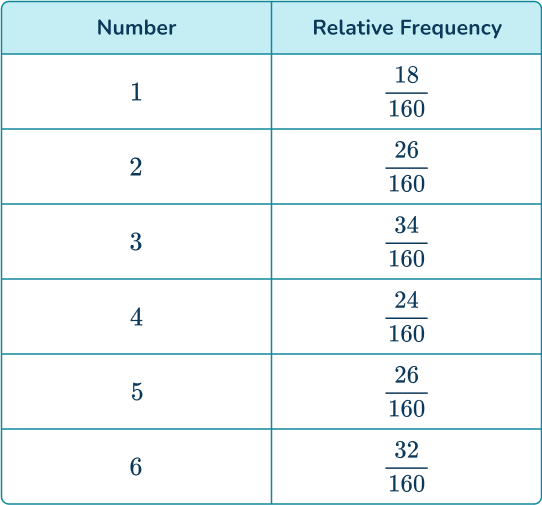
Dividing the frequencies of each number by 160, you get

3. A 3- sided spinner is spun and the results are recorded.

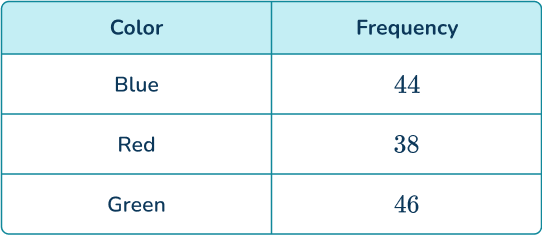
Find the probability distribution of the spinner, giving your answers as decimals to 2 decimal places.

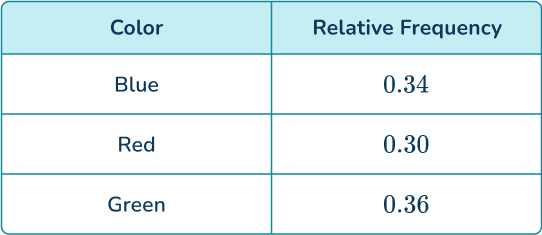
By dividing the frequencies of each color by 128 and simplifying, you have

4. A 3- sided spinner is spun and the results are recorded.

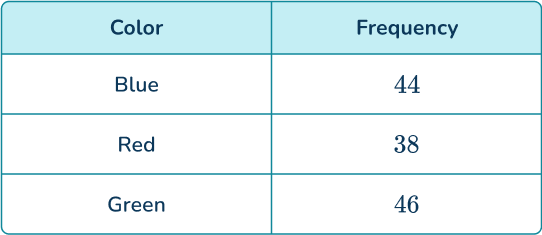
Find the probability of the spinner not landing on red. Give your answer as a fraction.

Add the frequencies of blue and green and divide by 128.

5. A card is picked at random from a deck and then replaced. This was repeated 4,000 times. The probability distribution of the experiment is given below.

How many times was a club picked?

6. Find the missing frequency from the probability distribution.

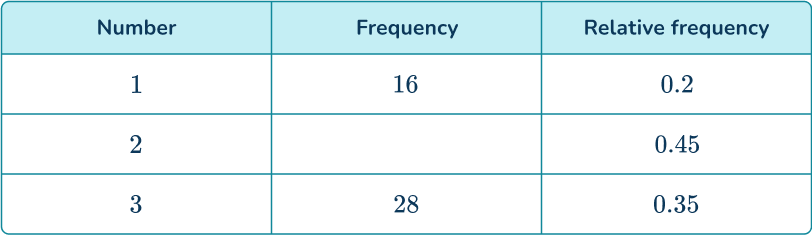
The total frequency is calculated by dividing the frequency by the relative frequency.

Experimental probability FAQs

Experimental probability is the likelihood of an event occurring based on the results of an actual experiment or trial. It is calculated as the ratio of the number of favorable outcomes to the total number of trials.

To calculate experimental probability, you calculate the relative frequency of the event: \text{Relative frequency}=\frac{\text{Frequency of event occurring}}{\text{Total number of trials of the experiment}}

Experimental Probability is based on actual results from an experiment or trial. Theoretical Probability is based on the possible outcomes of an event, calculated using probability rules and formulas without conducting experiments.

It helps us understand how likely events are in real-world scenarios based on actual data. For example, it can be used to predict outcomes in various fields such as social science, medicine, finance, and engineering.

The next lessons are

• Units of measurement
• Represent and interpret data

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

• The Basic math blog
• Member Login
• Pre-Algebra Lessons
• Pre-Algebra Word Problems
• Pre-Algebra Calculators
• Algebra Lessons
• Algebra Word Problems
• Algebra Proofs
• Advanced Algebra
• Algebra Calculators
• Geometry Lessons
• Geometry Word Problems
• Geometry Proofs
• Geometry Calculators
• Trigonometry Lessons
• Numeration System
• Basic Concepts of Set Theory
• Consumer Math
• Baseball Math
• Math for Nurses
• Statistics Made Easy
• High School Physics
• Basic Mathematics Store
• Math Vocabulary Quizzes
• SAT Math Prep
• Math Skills by Grade Level
• Ask an Expert
• Other Websites
• K-12 Worksheets
• Worksheets Generator
• Algebra Worksheets
• Geometry Worksheets
• Fun Online Math Games
• Pre-Algebra Games
• Math Puzzles
• Math Tricks

Experimental probability

Experimental probability (EP), also called empirical probability or relative frequency , is probability based on data collected from repeated trials.

Experimental probability formula

Let n represent the total number of trials or the number of times an experiment is done. Let p represent the number of times an event occurred while performing this experiment n times.

Example #1: A manufacturer makes 50,000 cell phones every month. After inspecting 1000 phones, the manufacturer found that 20 phones are defective. What is the probability that you will buy a phone that is defective? Predict how many phones will be defective next month.

The total number of times the experiment is conducted is n = 1000

The number of times an event occurred is p  = 20 

Experimental probability is performed when authorities want to know how the public feels about a matter. Since it is not possible to ask every single person in the country, they may conduct a survey by asking a sample of the entire population. This is called population sampling. Example #2 is an example of this situation.

There are about 319 million people living in the USA. Pretend that a survey of 1 million people revealed that 300,000 people think that all cars should be electric. What is the probability that someone chosen randomly does not like electric car? How many people like electric cars?

Notice that the number of people who do not like electric cars is 1000000 - 300000 = 700000

Difference between experimental probability and theoretical probability

You can argue the same thing using a die, a coin, and a spinner. We will though use a coin and a spinner to help you see the difference.

Using a coin 

In theoretical probability, we say that "each outcome is equally likely " without the actual experiment. For instance, without  flipping a coin, you know that the outcome could either be heads or tails.  If the coin is not altered, we argue that each outcome (heads or tails) is equally likely. In other words, we are saying that in theory or (supposition, conjecture, speculation, assumption, educated guess) the probability to get heads is 50% or the probability to get tails in 50%. Since you did not actually flip the coin, you are making an assumption based on logic.

The logic is that there are 2 possible outcomes and since you are choosing 1 of the 2 outcomes, the probability is 1/2 or 50%. This is theoretical probability or guessing probability or probability based on assumption.

In the example above about flipping a coin, suppose you are looking for the probability to get a head. 

Then, the number of favorable outcomes is 1 and the number of possible outcomes is 2.

In experimental probability,  we want to take the guess work out of the picture, by doing the experiment to see how many times heads or teals will come up. If you flip a coin 1000 times, you might realize that it landed on heads only 400 times. In this case, the probability to get heads is only 40%. 

Your experiment may not even show tails until after the 4th flip and yet in the end you ended up with more tails than heads. 

If you repeat the experiment another day, you may find a completely different result. May be this time the number of heads is 600 and the number of tails is 400.

Using a spinner

Suppose a spinner has four equal-sized sections that are red, green, black, and yellow. 

In theoretical probability, you will not spin the spinner. Instead, you will say that the probability to get green is one-fourth or 25%. Why 25%? The total number of outcomes is 4 and the number of favorable outcomes is 1.

1/4 = 0.25 = 25%

However, in experimental probability, you may decide to spin the spinner 50 times or even more to see how many times you will get each color.

Suppose you spin the spinner 50 times. It is quite possible that you may end up with the result shown below:

Red: 10 Green: 15 Black: 5 Yellow: 20

Now, the probability to get green is 15/50 = 0.3 = 30%

As you can see, experimental probability is based more on facts, data collected, experiment or research!

Theoretical probability

Special Math Topics

Applied math.

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved