in an experiment on photoelectric effect the graph between

Introduction to Quantum Physics

The photoelectric effect, learning objectives.

By the end of this section, you will be able to:

• Describe a typical photoelectric-effect experiment.
• Determine the maximum kinetic energy of photoelectrons ejected by photons of one energy or wavelength, when given the maximum kinetic energy of photoelectrons for a different photon energy or wavelength.

When light strikes materials, it can eject electrons from them. This is called the photoelectric effect , meaning that light ( photo ) produces electricity. One common use of the photoelectric effect is in light meters, such as those that adjust the automatic iris on various types of cameras. In a similar way, another use is in solar cells, as you probably have in your calculator or have seen on a roof top or a roadside sign. These make use of the photoelectric effect to convert light into electricity for running different devices.

Figure 1. The photoelectric effect can be observed by allowing light to fall on the metal plate in this evacuated tube. Electrons ejected by the light are collected on the collector wire and measured as a current. A retarding voltage between the collector wire and plate can then be adjusted so as to determine the energy of the ejected electrons. For example, if it is sufficiently negative, no electrons will reach the wire. (credit: P.P. Urone)

This effect has been known for more than a century and can be studied using a device such as that shown in Figure 1. This figure shows an evacuated tube with a metal plate and a collector wire that are connected by a variable voltage source, with the collector more negative than the plate. When light (or other EM radiation) strikes the plate in the evacuated tube, it may eject electrons. If the electrons have energy in electron volts (eV) greater than the potential difference between the plate and the wire in volts, some electrons will be collected on the wire. Since the electron energy in eV is eV , where q is the electron charge and V is the potential difference, the electron energy can be measured by adjusting the retarding voltage between the wire and the plate. The voltage that stops the electrons from reaching the wire equals the energy in eV. For example, if –3.00 V barely stops the electrons, their energy is 3.00 eV. The number of electrons ejected can be determined by measuring the current between the wire and plate. The more light, the more electrons; a little circuitry allows this device to be used as a light meter.

What is really important about the photoelectric effect is what Albert Einstein deduced from it. Einstein realized that there were several characteristics of the photoelectric effect that could be explained only if EM radiation is itself quantized : the apparently continuous stream of energy in an EM wave is actually composed of energy quanta called photons. In his explanation of the photoelectric effect, Einstein defined a quantized unit or quantum of EM energy, which we now call a photon , with an energy proportional to the frequency of EM radiation. In equation form, the photon energy is  E  =  hf , where E is the energy of a photon of frequency f and h is Planck’s constant. This revolutionary idea looks similar to Planck’s quantization of energy states in blackbody oscillators, but it is quite different. It is the quantization of EM radiation itself. EM waves are composed of photons and are not continuous smooth waves as described in previous chapters on optics. Their energy is absorbed and emitted in lumps, not continuously. This is exactly consistent with Planck’s quantization of energy levels in blackbody oscillators, since these oscillators increase and decrease their energy in steps of hf  by absorbing and emitting photons having  E  =  hf . We do not observe this with our eyes, because there are so many photons in common light sources that individual photons go unnoticed. (See Figure 2.) The next section of the text ( Photon Energies and the Electromagnetic Spectrum ) is devoted to a discussion of photons and some of their characteristics and implications. For now, we will use the photon concept to explain the photoelectric effect, much as Einstein did.

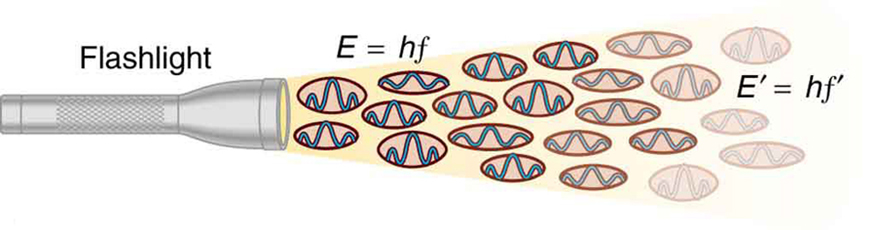
Figure 2. An EM wave of frequency f is composed of photons, or individual quanta of EM radiation. The energy of each photon is E  = hf , where h is Planck’s constant and f is the frequency of the EM radiation. Higher intensity means more photons per unit area. The flashlight emits large numbers of photons of many different frequencies, hence others have energy E ′ =  hf ′, and so on.

The photoelectric effect has the properties discussed below. All these properties are consistent with the idea that individual photons of EM radiation are absorbed by individual electrons in a material, with the electron gaining the photon’s energy. Some of these properties are inconsistent with the idea that EM radiation is a simple wave. For simplicity, let us consider what happens with monochromatic EM radiation in which all photons have the same energy hf .

• If we vary the frequency of the EM radiation falling on a material, we find the following: For a given material, there is a threshold frequency f 0 for the EM radiation below which no electrons are ejected, regardless of intensity. Individual photons interact with individual electrons. Thus if the photon energy is too small to break an electron away, no electrons will be ejected. If EM radiation was a simple wave, sufficient energy could be obtained by increasing the intensity.
• Once EM radiation falls on a material, electrons are ejected without delay . As soon as an individual photon of a sufficiently high frequency is absorbed by an individual electron, the electron is ejected. If the EM radiation were a simple wave, several minutes would be required for sufficient energy to be deposited to the metal surface to eject an electron.
• The number of electrons ejected per unit time is proportional to the intensity of the EM radiation and to no other characteristic. High-intensity EM radiation consists of large numbers of photons per unit area, with all photons having the same characteristic energy hf .
• If we vary the intensity of the EM radiation and measure the energy of ejected electrons, we find the following: The maximum kinetic energy of ejected electrons is independent of the intensity of the EM radiation . Since there are so many electrons in a material, it is extremely unlikely that two photons will interact with the same electron at the same time, thereby increasing the energy given it. Instead (as noted in 3 above), increased intensity results in more electrons of the same energy being ejected. If EM radiation were a simple wave, a higher intensity could give more energy, and higher-energy electrons would be ejected.
• The kinetic energy of an ejected electron equals the photon energy minus the binding energy of the electron in the specific material. An individual photon can give all of its energy to an electron. The photon’s energy is partly used to break the electron away from the material. The remainder goes into the ejected electron’s kinetic energy. In equation form, this is given by KE e  =  hf  − BE, where KE e is the maximum kinetic energy of the ejected electron, hf  is the photon’s energy, and BE is the binding energy of the electron to the particular material. (BE is sometimes called the work function of the material.) This equation, due to Einstein in 1905, explains the properties of the photoelectric effect quantitatively. An individual photon of EM radiation (it does not come any other way) interacts with an individual electron, supplying enough energy, BE, to break it away, with the remainder going to kinetic energy. The binding energy is BE =  hf 0 , where f 0 is the threshold frequency for the particular material. Figure 3 shows a graph of maximum KE e versus the frequency of incident EM radiation falling on a particular material.

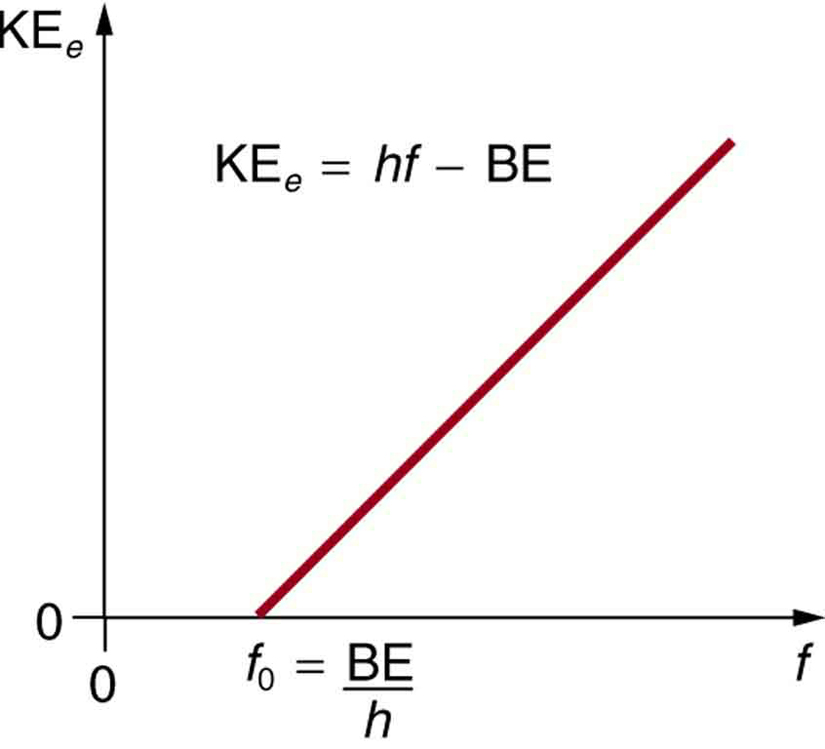
Figure 3. Photoelectric effect. A graph of the kinetic energy of an ejected electron, KE e , versus the frequency of EM radiation impinging on a certain material. There is a threshold frequency below which no electrons are ejected, because the individual photon interacting with an individual electron has insufficient energy to break it away. Above the threshold energy, KE e increases linearly with f , consistent with KE e = hf − BE. The slope of this line is h —the data can be used to determine Planck’s constant experimentally. Einstein gave the first successful explanation of such data by proposing the idea of photons—quanta of EM radiation.

Einstein’s idea that EM radiation is quantized was crucial to the beginnings of quantum mechanics. It is a far more general concept than its explanation of the photoelectric effect might imply. All EM radiation can also be modeled in the form of photons, and the characteristics of EM radiation are entirely consistent with this fact. (As we will see in the next section, many aspects of EM radiation, such as the hazards of ultraviolet (UV) radiation, can be explained only by photon properties.) More famous for modern relativity, Einstein planted an important seed for quantum mechanics in 1905, the same year he published his first paper on special relativity. His explanation of the photoelectric effect was the basis for the Nobel Prize awarded to him in 1921. Although his other contributions to theoretical physics were also noted in that award, special and general relativity were not fully recognized in spite of having been partially verified by experiment by 1921. Although hero-worshipped, this great man never received Nobel recognition for his most famous work—relativity.

Example 1. Calculating Photon Energy and the Photoelectric Effect: A Violet Light

1. What is the energy in joules and electron volts of a photon of 420-nm violet light?

2. What is the maximum kinetic energy of electrons ejected from calcium by 420-nm violet light, given that the binding energy (or work function) of electrons for calcium metal is 2.71 eV?

To solve Part 1, note that the energy of a photon is given by E  =  hf . For Part 2, once the energy of the photon is calculated, it is a straightforward application of KE e  =  hf  − BE to find the ejected electron’s maximum kinetic energy, since BE is given.

Solution for Part 1

Photon energy is given by  E  =  hf .

Since we are given the wavelength rather than the frequency, we solve the familiar relationship c  =  fλ for the frequency, yielding [latex]f=\frac{c}{\lambda}\\[/latex].

Combining these two equations gives the useful relationship [latex]E=\frac{hc}{\lambda}\\[/latex].

Now substituting known values yields

[latex]\displaystyle{E}=\frac{\left(6.63\times10^{-34}\text{ J}\cdot\text{ s}\right)\left(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}=4.74\times10^{-19}\text{ J}\\[/latex]

Converting to eV, the energy of the photon is

[latex]\displaystyle{E}=\left(4.47\times10^{-19}\text{ J}\right)\frac{1\text{ eV}}{1.6\times10^{-19}\text{ J}}=2.96\text{ eV}\\[/latex]

Solution for Part 2

Finding the kinetic energy of the ejected electron is now a simple application of the equation KE e  =  hf  − BE. Substituting the photon energy and binding energy yields KE e  =  hf  − BE = 2.96 eV − 2.71 eV = 0.246 eV.

The energy of this 420-nm photon of violet light is a tiny fraction of a joule, and so it is no wonder that a single photon would be difficult for us to sense directly—humans are more attuned to energies on the order of joules. But looking at the energy in electron volts, we can see that this photon has enough energy to affect atoms and molecules. A DNA molecule can be broken with about 1 eV of energy, for example, and typical atomic and molecular energies are on the order of eV, so that the UV photon in this example could have biological effects. The ejected electron (called a photoelectron ) has a rather low energy, and it would not travel far, except in a vacuum. The electron would be stopped by a retarding potential of but 0.26 eV. In fact, if the photon wavelength were longer and its energy less than 2.71 eV, then the formula would give a negative kinetic energy, an impossibility. This simply means that the 420-nm photons with their 2.96-eV energy are not much above the frequency threshold. You can show for yourself that the threshold wavelength is 459 nm (blue light). This means that if calcium metal is used in a light meter, the meter will be insensitive to wavelengths longer than those of blue light. Such a light meter would be completely insensitive to red light, for example.

PhET Explorations: Photoelectric Effect

See how light knocks electrons off a metal target, and recreate the experiment that spawned the field of quantum mechanics.

Click to download the simulation. Run using Java.

Section Summary

• The photoelectric effect is the process in which EM radiation ejects electrons from a material.
• Einstein proposed photons to be quanta of EM radiation having energy E   =  hf , where f  is the frequency of the radiation.
• All EM radiation is composed of photons. As Einstein explained, all characteristics of the photoelectric effect are due to the interaction of individual photons with individual electrons.
• The maximum kinetic energy KE e  of ejected electrons (photoelectrons) is given by KE e  =  hf  − BE, where hf  is the photon energy and BE is the binding energy (or work function) of the electron to the particular material.

Conceptual Questions

• Is visible light the only type of EM radiation that can cause the photoelectric effect?
• Which aspects of the photoelectric effect cannot be explained without photons? Which can be explained without photons? Are the latter inconsistent with the existence of photons?
• Is the photoelectric effect a direct consequence of the wave character of EM radiation or of the particle character of EM radiation? Explain briefly.
• Insulators (nonmetals) have a higher BE than metals, and it is more difficult for photons to eject electrons from insulators. Discuss how this relates to the free charges in metals that make them good conductors.
• If you pick up and shake a piece of metal that has electrons in it free to move as a current, no electrons fall out. Yet if you heat the metal, electrons can be boiled off. Explain both of these facts as they relate to the amount and distribution of energy involved with shaking the object as compared with heating it.

Problems & Exercises

• What is the longest-wavelength EM radiation that can eject a photoelectron from silver, given that the binding energy is 4.73 eV? Is this in the visible range?
• Find the longest-wavelength photon that can eject an electron from potassium, given that the binding energy is 2.24 eV. Is this visible EM radiation?
• What is the binding energy in eV of electrons in magnesium, if the longest-wavelength photon that can eject electrons is 337 nm?
• Calculate the binding energy in eV of electrons in aluminum, if the longest-wavelength photon that can eject them is 304 nm.
• What is the maximum kinetic energy in eV of electrons ejected from sodium metal by 450-nm EM radiation, given that the binding energy is 2.28 eV?
• UV radiation having a wavelength of 120 nm falls on gold metal, to which electrons are bound by 4.82 eV. What is the maximum kinetic energy of the ejected photoelectrons?
• Violet light of wavelength 400 nm ejects electrons with a maximum kinetic energy of 0.860 eV from sodium metal. What is the binding energy of electrons to sodium metal?
• UV radiation having a 300-nm wavelength falls on uranium metal, ejecting 0.500-eV electrons. What is the binding energy of electrons to uranium metal?
• (a) What is the wavelength of EM radiation that ejects 2.00-eV electrons from calcium metal, given that the binding energy is 2.71 eV? (b) What type of EM radiation is this?
• Find the wavelength of photons that eject 0.100-eV electrons from potassium, given that the binding energy is 2.24 eV. Are these photons visible?
• What is the maximum velocity of electrons ejected from a material by 80-nm photons, if they are bound to the material by 4.73 eV?
• Photoelectrons from a material with a binding energy of 2.71 eV are ejected by 420-nm photons. Once ejected, how long does it take these electrons to travel 2.50 cm to a detection device?
• A laser with a power output of 2.00 mW at a wavelength of 400 nm is projected onto calcium metal. (a) How many electrons per second are ejected? (b) What power is carried away by the electrons, given that the binding energy is 2.71 eV?
• (a) Calculate the number of photoelectrons per second ejected from a 1.00-mm 2 area of sodium metal by 500-nm EM radiation having an intensity of 1.30 kW/m 2 (the intensity of sunlight above the Earth’s atmosphere). (b) Given that the binding energy is 2.28 eV, what power is carried away by the electrons? (c) The electrons carry away less power than brought in by the photons. Where does the other power go? How can it be recovered?
• Unreasonable Results.  Red light having a wavelength of 700 nm is projected onto magnesium metal to which electrons are bound by 3.68 eV. (a) Use KE e  =  hf  − BE to calculate the kinetic energy of the ejected electrons. (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
• Unreasonable Results.  (a) What is the binding energy of electrons to a material from which 4.00-eV electrons are ejected by 400-nm EM radiation? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

photoelectric effect:  the phenomenon whereby some materials eject electrons when light is shined on them

photon:  a quantum, or particle, of electromagnetic radiation

photon energy:  the amount of energy a photon has; E  =  hf

binding energy:  also called the work function; the amount of energy necessary to eject an electron from a material

Selected Solutions to Problems & Exercises

5. 0.483 eV

9. (a) 264 nm; (b) Ultraviolet

11. 1.95 × 10 6 m/s

13. (a) 4.02 × 10 15 s; (b) 0.256 mW

15. (a) −1.90 eV; (b) Negative kinetic energy; (c) That the electrons would be knocked free.

• College Physics. Authored by : OpenStax College. Located at : http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a/College_Physics . License : CC BY: Attribution . License Terms : Located at License
• PhET Interactive Simulations . Provided by : University of Colorado Boulder . Located at : http://phet.colorado.edu . License : CC BY: Attribution

Photoelectric Effect ( College Board AP® Chemistry )

Study guide.

Chemistry Content Creator

One of the main characteristics of light is its wave-particle duality

This means that light can behave as a wave, but also as a particle

As seen in previous sections, a light wave has frequency , wavelength and energy

However, the discovery of the photoelectric effect suggested that light can also behaves as a particle

The photoelectric effect was observed when some metals emit electrons when light was shone on them

The results of this experiment suggested that light must come into particles

A light particle is called a photon

Absorption and Emission of photons

Electrons move around the nucleus of the atoms in energy shells

Atoms and molecules can absorb photons, and the electrons will jump to higher energy shells

When this occurs, the energy of the atom or molecule increases by an amount equal to the energy of the photon

A moment later, a photon will be emitted, and the electrons will return to their original shell which is also called the ground state

When this occurs, the energy of the atom or molecule will decrease by an amount equal to the energy of the photon

Absorption and Emission diagram

The difference between absorption and emission depends on whether electrons are jumping from lower to higher energy levels or the other way around

The Hydrogen Emission Spectrum

Niels Bohr constructed the hydrogen emission spectrum where he showed the energy released when electrons jump from higher shells to lower shells

Bohr suggested that electrons can only exist in fixed energy shells

This means that electronic transitions can only occur when photons with an specific amount of energy are absorbed or released

Each electronic transition has to do with photons from specific regions of the electromagnetic spectrum

Regions of the electromagnetic spectrum 

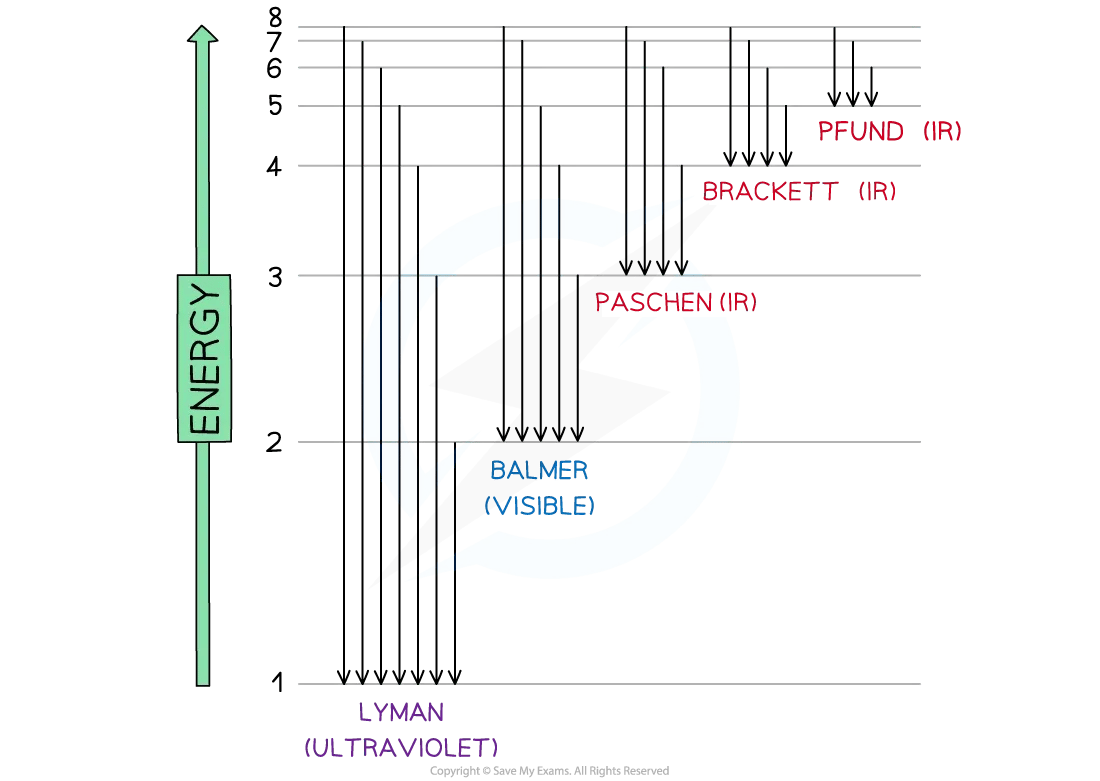
Electron jumps in the hydrogen spectrum

The jumps can be summarized in table below:

Electron transitions summary

Energy of Photons

Frequency, wavelength and energy.

As it was shown in the electromagnetic spectrum, the shorter the frequency of an electromagnetic wave, the longer its wavelength

Frequency ( ν ) and wavelength ( λ ) are inversely proportional

The equation that links them is:

In this equation c is the speed of light which is 2.998 x 10 8 ms -1

The spectrum also shows that, the shorter the frequency, the lower the energy of the radiation

Frequency ( ν ) and energy ( E) are directly proportional

In this equation h is the Planck’s constant , which is 6.626 x 10 -34 J s

These two equations can be used to calculate frequency, wavelength or energy when one of them is given

Examiner Tip

Both equations and constants can be found in the AP Chemistry Constants and Equations section in your examination

Worked Example

Calculate the wavelength of the photon emitted when an electron transition has released 1.632 x 10 -18 J

Step 1: Calculate the frequency of the photon by using the Planck’s equation

v = 2.463 × 10 15 s -1 

Step 2: Use the frequency calculated in Step 1 to calculate the wavelength of the photon

λ = 1.217 × 10 -7 m

You've read 0 of your 10 free study guides

Unlock more, it's free, join the 100,000 + students that ❤️ save my exams.

the (exam) results speak for themselves:

Did this page help you?

• Spectroscopy
• Chemical Changes
• Stoichiometry
• Types of Chemical Reactions
• Brønsted-Lowry Acids & Bases
• Reaction Rates
• Reaction Mechanisms
• Calorimetry
• Enthalpy Changes
• Equilibrium Constants

Author: Martín

Expertise: Chemistry Content Creator

Martín, a dedicated chemistry teacher and tutor, excels in guiding students through IB, AP, and IGCSE Chemistry. As an IB Chemistry student, he came from hands-on preparation, focusing on practical exam techniques and rigorous practice. While at Universidad San Francisco de Quito, his academic journey sparked a passion for computational and physical chemistry. Martín specializes in chemistry, and he knows that SaveMyExams is the right place if he wants to have a positive impact all around the world.

29.2 The Photoelectric Effect

Learning objectives.

By the end of this section, you will be able to:

• Describe a typical photoelectric-effect experiment.
• Determine the maximum kinetic energy of photoelectrons ejected by photons of one energy or wavelength, when given the maximum kinetic energy of photoelectrons for a different photon energy or wavelength.

When light strikes materials, it can eject electrons from them. This is called the photoelectric effect , meaning that light ( photo ) produces electricity. One common use of the photoelectric effect is in light meters, such as those that adjust the automatic iris on various types of cameras. In a similar way, another use is in solar cells, as you probably have in your calculator or have seen on a roof top or a roadside sign. These make use of the photoelectric effect to convert light into electricity for running different devices.

This effect has been known for more than a century and can be studied using a device such as that shown in Figure 29.6 . This figure shows an evacuated tube with a metal plate and a collector wire that are connected by a variable voltage source, with the collector more negative than the plate. When light (or other EM radiation) strikes the plate in the evacuated tube, it may eject electrons. If the electrons have energy in electron volts (eV) greater than the potential difference between the plate and the wire in volts, some electrons will be collected on the wire. Since the electron energy in eV is qV qV , where q q is the electron charge and V V is the potential difference, the electron energy can be measured by adjusting the retarding voltage between the wire and the plate. The voltage that stops the electrons from reaching the wire equals the energy in eV. For example, if –3.00 V –3.00 V barely stops the electrons, their energy is 3.00 eV. The number of electrons ejected can be determined by measuring the current between the wire and plate. The more light, the more electrons; a little circuitry allows this device to be used as a light meter.

What is really important about the photoelectric effect is what Albert Einstein deduced from it. Einstein realized that there were several characteristics of the photoelectric effect that could be explained only if EM radiation is itself quantized : the apparently continuous stream of energy in an EM wave is actually composed of energy quanta called photons. In his explanation of the photoelectric effect, Einstein defined a quantized unit or quantum of EM energy, which we now call a photon , with an energy proportional to the frequency of EM radiation. In equation form, the photon energy is

where E E is the energy of a photon of frequency f f and h h is Planck’s constant. This revolutionary idea looks similar to Planck’s quantization of energy states in blackbody oscillators, but it is quite different. It is the quantization of EM radiation itself. EM waves are composed of photons and are not continuous smooth waves as described in previous chapters on optics. Their energy is absorbed and emitted in lumps, not continuously. This is exactly consistent with Planck’s quantization of energy levels in blackbody oscillators, since these oscillators increase and decrease their energy in steps of hf hf by absorbing and emitting photons having E = hf E = hf . We do not observe this with our eyes, because there are so many photons in common light sources that individual photons go unnoticed. (See Figure 29.7 .) The next section of the text ( Photon Energies and the Electromagnetic Spectrum ) is devoted to a discussion of photons and some of their characteristics and implications. For now, we will use the photon concept to explain the photoelectric effect, much as Einstein did.

The photoelectric effect has the properties discussed below. All these properties are consistent with the idea that individual photons of EM radiation are absorbed by individual electrons in a material, with the electron gaining the photon’s energy. Some of these properties are inconsistent with the idea that EM radiation is a simple wave. For simplicity, let us consider what happens with monochromatic EM radiation in which all photons have the same energy hf hf .

• If we vary the frequency of the EM radiation falling on a material, we find the following: For a given material, there is a threshold frequency f 0 f 0 for the EM radiation below which no electrons are ejected, regardless of intensity. Individual photons interact with individual electrons. Thus if the photon energy is too small to break an electron away, no electrons will be ejected. If EM radiation was a simple wave, sufficient energy could be obtained by increasing the intensity.
• Once EM radiation falls on a material, electrons are ejected without delay . As soon as an individual photon of a sufficiently high frequency is absorbed by an individual electron, the electron is ejected. If the EM radiation were a simple wave, several minutes would be required for sufficient energy to be deposited to the metal surface to eject an electron.
• The number of electrons ejected per unit time is proportional to the intensity of the EM radiation and to no other characteristic. High-intensity EM radiation consists of large numbers of photons per unit area, with all photons having the same characteristic energy hf hf .
• If we vary the intensity of the EM radiation and measure the energy of ejected electrons, we find the following: The maximum kinetic energy of ejected electrons is independent of the intensity of the EM radiation . Since there are so many electrons in a material, it is extremely unlikely that two photons will interact with the same electron at the same time, thereby increasing the energy given it. Instead (as noted in 3 above), increased intensity results in more electrons of the same energy being ejected. If EM radiation were a simple wave, a higher intensity could give more energy, and higher-energy electrons would be ejected.
• The kinetic energy of an ejected electron equals the photon energy minus the binding energy of the electron in the specific material. An individual photon can give all of its energy to an electron. The photon’s energy is partly used to break the electron away from the material. The remainder goes into the ejected electron’s kinetic energy. In equation form, this is given by KE e = hf − BE , KE e = hf − BE , 29.5 where KE e KE e is the maximum kinetic energy of the ejected electron, hf hf is the photon’s energy, and BE is the binding energy of the electron to the particular material. (BE is sometimes called the work function of the material.) This equation, due to Einstein in 1905, explains the properties of the photoelectric effect quantitatively. An individual photon of EM radiation (it does not come any other way) interacts with an individual electron, supplying enough energy, BE, to break it away, with the remainder going to kinetic energy. The binding energy is BE = hf 0 BE = hf 0 , where f 0 f 0 is the threshold frequency for the particular material. Figure 29.8 shows a graph of maximum KE e KE e versus the frequency of incident EM radiation falling on a particular material.

Einstein’s idea that EM radiation is quantized was crucial to the beginnings of quantum mechanics. It is a far more general concept than its explanation of the photoelectric effect might imply. All EM radiation can also be modeled in the form of photons, and the characteristics of EM radiation are entirely consistent with this fact. (As we will see in the next section, many aspects of EM radiation, such as the hazards of ultraviolet (UV) radiation, can be explained only by photon properties.) More famous for modern relativity, Einstein planted an important seed for quantum mechanics in 1905, the same year he published his first paper on special relativity. His explanation of the photoelectric effect was the basis for the Nobel Prize awarded to him in 1921. Although his other contributions to theoretical physics were also noted in that award, special and general relativity were not fully recognized in spite of having been partially verified by experiment by 1921. Although hero-worshipped, this great man never received Nobel recognition for his most famous work—relativity.

Example 29.1

Calculating photon energy and the photoelectric effect: a violet light.

(a) What is the energy in joules and electron volts of a photon of 420-nm violet light? (b) What is the maximum kinetic energy of electrons ejected from calcium by 420-nm violet light, given that the binding energy (or work function) of electrons for calcium metal is 2.71 eV?

To solve part (a), note that the energy of a photon is given by E = hf E = hf . For part (b), once the energy of the photon is calculated, it is a straightforward application of KE e = hf –BE KE e = hf –BE to find the ejected electron’s maximum kinetic energy, since BE is given.

Solution for (a)

Photon energy is given by

Since we are given the wavelength rather than the frequency, we solve the familiar relationship c = fλ c = fλ for the frequency, yielding

Combining these two equations gives the useful relationship

Now substituting known values yields

Converting to eV, the energy of the photon is

Solution for (b)

Finding the kinetic energy of the ejected electron is now a simple application of the equation KE e = hf –BE KE e = hf –BE . Substituting the photon energy and binding energy yields

The energy of this 420-nm photon of violet light is a tiny fraction of a joule, and so it is no wonder that a single photon would be difficult for us to sense directly—humans are more attuned to energies on the order of joules. But looking at the energy in electron volts, we can see that this photon has enough energy to affect atoms and molecules. A DNA molecule can be broken with about 1 eV of energy, for example, and typical atomic and molecular energies are on the order of eV, so that the UV photon in this example could have biological effects. The ejected electron (called a photoelectron ) has a rather low energy, and it would not travel far, except in a vacuum. The electron would be stopped by a retarding potential of but 0.26 eV. In fact, if the photon wavelength were longer and its energy less than 2.71 eV, then the formula would give a negative kinetic energy, an impossibility. This simply means that the 420-nm photons with their 2.96-eV energy are not much above the frequency threshold. You can show for yourself that the threshold wavelength is 459 nm (blue light). This means that if calcium metal is used in a light meter, the meter will be insensitive to wavelengths longer than those of blue light. Such a light meter would be completely insensitive to red light, for example.

PhET Explorations

Photoelectric effect.

See how light knocks electrons off a metal target, and recreate the experiment that spawned the field of quantum mechanics.

Click to view content .

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/29-2-the-photoelectric-effect

© Jul 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Lecture Demonstration Manual
• Lab Manuals
• Instructional Videos
• PhotoSpheres

You are here

Table of contents.

• Experiment 1 - Magnetic Fields of Coils and Faraday's Law
• Experiment 2 - Microwave Optics
• Experiment 3 - Geometrical Optics
• Experiment 4 - Physical Optics
• Experiment 5 - Fluids and Thermodynamics

Experiment 6 - The Photoelectric Effect

• Experiment 7 - Radioactivity
• Photodiode with amplifier
• Batteries to operate amplifier and provide reverse voltage
• Digital voltmeter to read reverse voltage
• Source of monochromatic light beams to irradiate photocathode
• Neutral filter to vary light intensity

INTRODUCTION

The energy quantization of electromagnetic radiation in general, and of light in particular, is expressed in the famous relation

\begin{eqnarray} E &=& hf, \label{eqn_1} \end{eqnarray}

where \(E\) is the energy of the radiation, \(f\) is its frequency, and \(h\) is Planck's constant (6.63×10 -34 Js). The notion of light quantization was first introduced by Planck. Its validity is based on solid experimental evidence, most notably the photoelectric effect . The basic physical process underlying this effect is the emission of electrons in metals exposed to light. There are four aspects of photoelectron emission which conflict with the classical view that the instantaneous intensity of electromagnetic radiation is given by the Poynting vector \(\textbf{S}\):

\begin{eqnarray} \textbf{S} &=& (\textbf{E}\times\textbf{B})/\mu_0, \label{eqn_2} \end{eqnarray}

with \(\textbf{E}\) and \(\textbf{B}\) the electric and magnetic fields of the radiation, respectively, and μ 0 (4π×10 -7 Tm/A) the permeability of free space. Specifically:

No photoelectrons are emitted from the metal when the incident light is below a minimum frequency, regardless of its intensity. (The value of the minimum frequency is unique to each metal.)

Photoelectrons are emitted from the metal when the incident light is above a threshold frequency. The kinetic energy of the emitted photoelectrons increases with the frequency of the light.

The number of emitted photoelectrons increases with the intensity of the incident light. However, the kinetic energy of these electrons is independent of the light intensity.

Photoemission is effectively instantaneous.

Consider the conduction electrons in a metal to be bound in a well-defined potential. The energy required to release an electron is called the work function \(W_0\) of the metal. In the classical model, a photoelectron could be released if the incident light had sufficient intensity. However, Eq. \eqref{eqn_1} requires that the light exceed a threshold frequency \(f_{\textrm{t}}\) for an electron to be emitted. If \(f > f_{\textrm{t}}\), then a single light quantum (called a photon ) of energy \(E = hf\) is sufficient to liberate an electron, and any residual energy carried by the photon is converted into the kinetic energy of the electron. Thus, from energy conservation, \(E = W_0 + K\), or

\begin{eqnarray} K &=& (1/2)mv^2 = E - W_0 = hf - W_0. \label{eqn_3} \end{eqnarray}

When the incident light intensity is increased, more photons are available for the release of electrons, and the magnitude of the photoelectric current increases. From Eq. \eqref{eqn_3}, we see that the kinetic energy of the electrons is independent of the light intensity and depends only on the frequency.

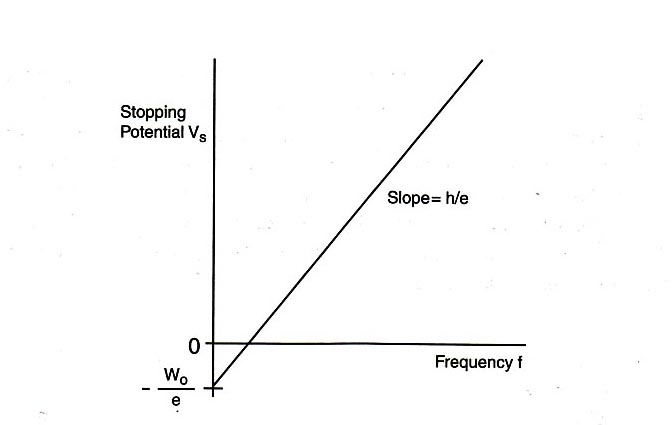
The photoelectric current in a typical setup is extremely small, and making a precise measurement is difficult. Normally the electrons will reach the anode of the photodiode, and their number can be measured from the (minute) anode current. However, we can apply a reverse voltage to the anode; this reverse voltage repels the electrons and prevents them from reaching the anode. The minimum required voltage is called the stopping potential \(V_{\textrm{s}}\), and the “stopping energy” of each electron is therefore \(eV_{\textrm{s}}\). Thus,

\begin{eqnarray} eV_{\textrm{s}} &=& hf - W_0, \label{eqn_4} \end{eqnarray}

\begin{eqnarray} V_{\textrm{s}} &=& (h/e)f - W_0/e. \label{eqn_5} \end{eqnarray}

Eq. \eqref{eqn_5} shows a linear relationship between the stopping potential \(V_{\textrm{s}}\) and the light frequency \(f\), with slope \(h/e\) and vertical intercept \(-W_0/e\). If the value of the electron charge \(e\) is known, then this equation provides a good method for determining Planck's constant \(h\). In this experiment, we will measure the stopping potential with modern electronics.

THE PHOTODIODE AND ITS READOUT

The central element of the apparatus is the photodiode tube. The diode has a window which allows light to enter, and the cathode is a clean metal surface. To prevent the collision of electrons with air molecules, the diode tube is evacuated.

The photodiode and its associated electronics have a small “capacitance” and develop a voltage as they become charged by the emitted electrons. When the voltage across this “capacitor” reaches the stopping potential of the cathode, the voltage difference between the cathode and anode (which is equal to the stopping potential) stabilizes.

To measure the stopping potential, we use a very sensitive amplifier which has an input impedance larger than 10 13 ohms. The amplifier enables us to investigate the minuscule number of photoelectrons that are produced.

It would take considerable time to discharge the anode at the completion of a measurement by the usual high-leakage resistance of the circuit components, as the input impedance of the amplifier is very high. To speed up this process, a shorting switch is provided; it is labeled “Push to Zero”. The amplifier output will not stay at 0 volts very long after the switch is released. However, the anode output does stabilize once the photoelectrons charge it up.

There are two 9-volt batteries already installed in the photodiode housing. To check the batteries, you can use a voltmeter to measure the voltage between the output ground terminal and each battery test terminal. The battery test points are located on the side panel. You should replace the batteries if the voltage is less than 6 volts.

THE MONOCHROMATIC LIGHT BEAMS

This experiment requires the use of several different monochromatic light beams, which can be obtained from the spectral lines that make up the radiation produced by excited mercury atoms. The light is formed by an electrical discharge in a thin glass tube containing mercury vapor, and harmful ultraviolet components are filtered out by the glass envelope. Mercury light has five narrow spectral lines in the visible region — yellow, green, blue, violet, and ultraviolet — which can be separated spatially by the process of diffraction. For this purpose, we use a high-quality diffraction grating with 6000 lines per centimeter. The desired wavelength is selected with the aid of a collimator, while the intensity can be varied with a set of neutral density filters. A color filter at the entrance of the photodiode is used to minimize room light.

The equipment consists of a mercury vapor light housed in a sturdy metal box, which also holds the transformer for the high voltage. The transformer is fed by a 115-volt power source from an ordinary wall outlet. In order to prevent the possibility of getting an electric shock from the high voltage, do not remove the cover from the unit when it is plugged in.

To facilitate mounting of the filters, the light box is equipped with rails on the front panel. The optical components include a fixed slit (called a light aperture) which is mounted over the output hole in the front cover of the light box. A lens focuses the aperture on the photodiode window. The diffraction grating is mounted on the same frame that holds the lens, which simplifies the setup somewhat. A “blazed” grating, which has a preferred orientation for maximal light transmission and is not fully symmetric, is used. Turn the grating around to verify that you have the optimal orientation.

The variable transmission filter consists of computer-generated patterns of dots and lines that vary the intensity of the incident light. The relative transmission percentages are 100%, 80%, 60%, 40%, and 20%.

INITIAL SETUP

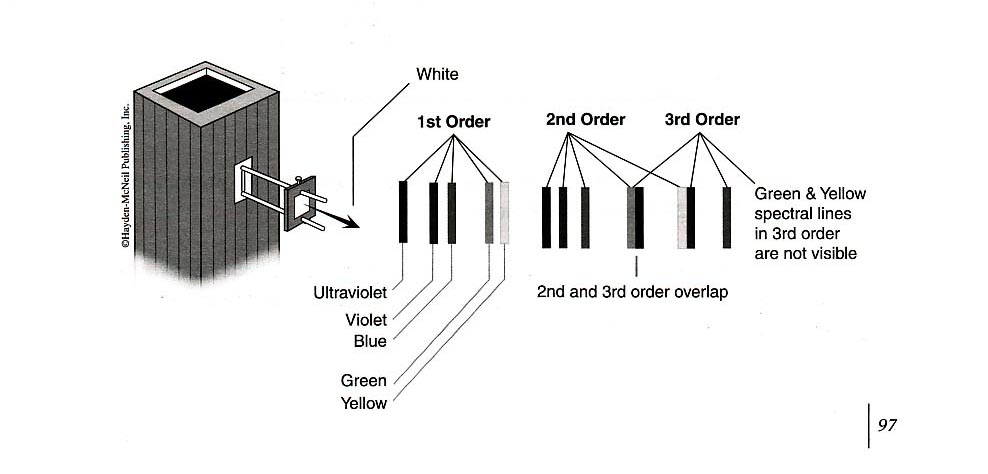
Your apparatus should be set up approximately like the figure above. Turn on the mercury lamp using the switch on the back of the light box. Swing the \(h/e\) apparatus box around on its arm, and you should see at various positions, yellow green, and several blue spectral lines on its front reflective mask. Notice that on one side of the imaginary “front-on” perpendicular line from the mercury lamp, the spectral lines are brighter than the similar lines from the other side. This is because the grating is “blazed”. In you experiments, use the first order spectrum on the side with the brighter lines.

Your apparatus should already be approximately aligned from previous experiments, but make the following alignment checks. Ask you TA for assistance if necessary.

Check the alignment of the mercury source and the aperture by looking at the light shining on the back of the grating. If necessary, adjust the back plate of the light-aperture assembly by loosening the two retaining screws and moving the plate to the left or right until the light shines directly on the center of the grating.

With the bright colored lines on the front reflective mask, adjust the lens/grating assembly on the mercury lamp light box until the lines are focused as sharply as possible.

Roll the round light shield (between the white screen and the photodiode housing) out of the way to view the photodiode window inside the housing. The phototube has a small square window for light to enter. When a spectral line is centered on the front mask, it should also be centered on this window. If not, rotate the housing until the image of the aperture is centered on the window, and fasten the housing. Return the round shield back into position to block stray light.

Connect the digital voltmeter (DVM) to the “Output” terminals of the photodiode. Select the 2 V or 20 V range on the meter.

Press the “Push to Zero” button on the side panel of the photodiode housing to short out any accumulated charge on the electronics. Note that the output will shift in the absence of light on the photodiode.

Record the photodiode output voltage on the DVM. This voltage is a direct measure of the stopping potential.

Use the green and yellow filters for the green and yellow mercury light. These filters block higher frequencies and eliminate ambient room light. In higher diffraction orders, they also block the ultraviolet light that falls on top of the yellow and green lines.

PROCEDURE PART 1: DEPENDENCE OF THE STOPPING POTENTIAL ON THE INTENSITY OF LIGHT

Adjust the angle of the photodiode-housing assembly so that the green line falls on the window of the photodiode.

Install the green filter and the round light shield.

Install the variable transmission filter on the collimator over the green filter such that the light passes through the section marked 100%. Record the photodiode output voltage reading on the DVM. Also determine the approximate recharge time after the discharge button has been pressed and released.

Repeat steps 1 – 3 for the other four transmission percentages, as well as for the ultraviolet light in second order.

Plot a graph of the stopping potential as a function of intensity.

PROCEDURE PART 2: DEPENDENCE OF THE STOPPING POTENTIAL ON THE FREQUENCY OF LIGHT

You can see five colors in the mercury light spectrum. The diffraction grating has two usable orders for deflection on one side of the center.

Adjust the photodiode-housing assembly so that only one color from the first-order diffraction pattern on one side of the center falls on the collimator.

For each color in the first order, record the photodiode output voltage reading on the DVM.

For each color in the second order, record the photodiode output voltage reading on the DVM.

Plot a graph of the stopping potential as a function of frequency, and determine the slope and the \(y\)-intercept of the graph. From this data, calculate \(W_0\) and \(h\). Compare this value of \(h\) with that provided in the “Introduction” section of this experiment.

Procedure Part 1:

Photodiode output voltage reading for 100% transmission =                                              

Approximate recharge time for 100% transmission =                                              

Photodiode output voltage reading for 80% transmission =                                              

Approximate recharge time for 80% transmission =                                              

Photodiode output voltage reading for 60% transmission =                                              

Approximate recharge time for 60% transmission =                                              

Photodiode output voltage reading for 40% transmission =                                              

Approximate recharge time for 40% transmission =                                              

Photodiode output voltage reading for 20% transmission =                                              

Approximate recharge time for 20% transmission =                                              

Photodiode output voltage reading for ultraviolet light =                                              

Approximate recharge time for ultraviolet light =                                              

Plot the graph of stopping potential as a function of intensity using one sheet of graph paper at the end of this workbook. Remember to label the axes and title the graph.

Procedure Part 2:

First-order diffraction pattern on one side of the center:

Photodiode output voltage reading for yellow light =                                              

Photodiode output voltage reading for green light =                                              

Photodiode output voltage reading for blue light =                                              

Photodiode output voltage reading for violet light =                                              

Second-order diffraction pattern on the other side of the center:

Plot the graph of stopping potential as a function of frequency using one sheet of graph paper at the end of this workbook. Remember to label the axes and title the graph.

Slope of graph =                                              

\(y\)-intercept of graph =                                              

\(W_0\) =                                              

\(h\) =                                              

Percentage difference between experimental and accepted values of \(h\) =                

{:instructional:lab_manuals:physics:6c:experiment_7:photo_graph_2.jpg|}}

Isaac Physics

You need to enable JavaScript to access Isaac Physics.