how to write null hypothesis ap bio

Null hypothesis

Null hypothesis n., plural: null hypotheses [nʌl haɪˈpɒθɪsɪs] Definition: a hypothesis that is valid or presumed true until invalidated by a statistical test

Table of Contents

Null Hypothesis Definition

Null hypothesis is defined as “the commonly accepted fact (such as the sky is blue) and researcher aim to reject or nullify this fact”.

More formally, we can define a null hypothesis as “a statistical theory suggesting that no statistical relationship exists between given observed variables” .

In biology , the null hypothesis is used to nullify or reject a common belief. The researcher carries out the research which is aimed at rejecting the commonly accepted belief.

What Is a Null Hypothesis?

A hypothesis is defined as a theory or an assumption that is based on inadequate evidence. It needs and requires more experiments and testing for confirmation. There are two possibilities that by doing more experiments and testing, a hypothesis can be false or true. It means it can either prove wrong or true (Blackwelder, 1982).

For example, Susie assumes that mineral water helps in the better growth and nourishment of plants over distilled water. To prove this hypothesis, she performs this experiment for almost a month. She watered some plants with mineral water and some with distilled water.

In a hypothesis when there are no statistically significant relationships among the two variables, the hypothesis is said to be a null hypothesis. The investigator is trying to disprove such a hypothesis. In the above example of plants, the null hypothesis is:

There are no statistical relationships among the forms of water that are given to plants for growth and nourishment.

Usually, an investigator tries to prove the null hypothesis wrong and tries to explain a relation and association between the two variables.

An opposite and reverse of the null hypothesis are known as the alternate hypothesis . In the example of plants the alternate hypothesis is:

There are statistical relationships among the forms of water that are given to plants for growth and nourishment.

The example below shows the difference between null vs alternative hypotheses:

Alternate Hypothesis: The world is round Null Hypothesis: The world is not round.

Copernicus and many other scientists try to prove the null hypothesis wrong and false. By their experiments and testing, they make people believe that alternate hypotheses are correct and true. If they do not prove the null hypothesis experimentally wrong then people will not believe them and never consider the alternative hypothesis true and correct.

The alternative and null hypothesis for Susie’s assumption is:

• Null Hypothesis: If one plant is watered with distilled water and the other with mineral water, then there is no difference in the growth and nourishment of these two plants.
• Alternative Hypothesis:  If one plant is watered with distilled water and the other with mineral water, then the plant with mineral water shows better growth and nourishment.

The null hypothesis suggests that there is no significant or statistical relationship. The relation can either be in a single set of variables or among two sets of variables.

Most people consider the null hypothesis true and correct. Scientists work and perform different experiments and do a variety of research so that they can prove the null hypothesis wrong or nullify it. For this purpose, they design an alternate hypothesis that they think is correct or true. The null hypothesis symbol is H 0 (it is read as H null or H zero ).

Why is it named the “Null”?

The name null is given to this hypothesis to clarify and explain that the scientists are working to prove it false i.e. to nullify the hypothesis. Sometimes it confuses the readers; they might misunderstand it and think that statement has nothing. It is blank but, actually, it is not. It is more appropriate and suitable to call it a nullifiable hypothesis instead of the null hypothesis.

Why do we need to assess it? Why not just verify an alternate one?

In science, the scientific method is used. It involves a series of different steps. Scientists perform these steps so that a hypothesis can be proved false or true. Scientists do this to confirm that there will be any limitation or inadequacy in the new hypothesis. Experiments are done by considering both alternative and null hypotheses, which makes the research safe. It gives a negative as well as a bad impact on research if a null hypothesis is not included or a part of the study. It seems like you are not taking your research seriously and not concerned about it and just want to impose your results as correct and true if the null hypothesis is not a part of the study.

Development of the Null

In statistics, firstly it is necessary to design alternate and null hypotheses from the given problem. Splitting the problem into small steps makes the pathway towards the solution easier and less challenging. how to write a null hypothesis?

Writing a null hypothesis consists of two steps:

• Firstly, initiate by asking a question.
• Secondly, restate the question in such a way that it seems there are no relationships among the variables.

In other words, assume in such a way that the treatment does not have any effect.

The usual recovery duration after knee surgery is considered almost 8 weeks.

A researcher thinks that the recovery period may get elongated if patients go to a physiotherapist for rehabilitation twice per week, instead of thrice per week, i.e. recovery duration reduces if the patient goes three times for rehabilitation instead of two times.

Step 1: Look for the problem in the hypothesis. The hypothesis either be a word or can be a statement. In the above example the hypothesis is:

“The expected recovery period in knee rehabilitation is more than 8 weeks”

Step 2: Make a mathematical statement from the hypothesis. Averages can also be represented as μ, thus the null hypothesis formula will be.

In the above equation, the hypothesis is equivalent to H1, the average is denoted by μ and > that the average is greater than eight.

Step 3: Explain what will come up if the hypothesis does not come right i.e., the rehabilitation period may not proceed more than 08 weeks.

There are two options: either the recovery will be less than or equal to 8 weeks.

H 0 : μ ≤ 8

In the above equation, the null hypothesis is equivalent to H 0 , the average is denoted by μ and ≤ represents that the average is less than or equal to eight.

What will happen if the scientist does not have any knowledge about the outcome?

Problem: An investigator investigates the post-operative impact and influence of radical exercise on patients who have operative procedures of the knee. The chances are either the exercise will improve the recovery or will make it worse. The usual time for recovery is 8 weeks.

Step 1: Make a null hypothesis i.e. the exercise does not show any effect and the recovery time remains almost 8 weeks.

H 0 : μ = 8

In the above equation, the null hypothesis is equivalent to H 0 , the average is denoted by μ, and the equal sign (=) shows that the average is equal to eight.

Step 2: Make the alternate hypothesis which is the reverse of the null hypothesis. Particularly what will happen if treatment (exercise) makes an impact?

In the above equation, the alternate hypothesis is equivalent to H1, the average is denoted by μ and not equal sign (≠) represents that the average is not equal to eight.

Significance Tests

To get a reasonable and probable clarification of statistics (data), a significance test is performed. The null hypothesis does not have data. It is a piece of information or statement which contains numerical figures about the population. The data can be in different forms like in means or proportions. It can either be the difference of proportions and means or any odd ratio.

The following table will explain the symbols:

P-value is the chief statistical final result of the significance test of the null hypothesis.

• P-value = Pr(data or data more extreme | H 0 true)
• | = “given”
• Pr = probability
• H 0 = the null hypothesis

The first stage of Null Hypothesis Significance Testing (NHST) is to form an alternate and null hypothesis. By this, the research question can be briefly explained.

Null Hypothesis = no effect of treatment, no difference, no association Alternative Hypothesis = effective treatment, difference, association

When to reject the null hypothesis?

Researchers will reject the null hypothesis if it is proven wrong after experimentation. Researchers accept null hypothesis to be true and correct until it is proven wrong or false. On the other hand, the researchers try to strengthen the alternate hypothesis. The binomial test is performed on a sample and after that, a series of tests were performed (Frick, 1995).

Step 1: Evaluate and read the research question carefully and consciously and make a null hypothesis. Verify the sample that supports the binomial proportion. If there is no difference then find out the value of the binomial parameter.

Show the null hypothesis as:

H 0 :p= the value of p if H 0 is true

To find out how much it varies from the proposed data and the value of the null hypothesis, calculate the sample proportion.

Step 2: In test statistics, find the binomial test that comes under the null hypothesis. The test must be based on precise and thorough probabilities. Also make a list of pmf that apply, when the null hypothesis proves true and correct.

When H 0 is true, X~b(n, p)

N = size of the sample

P = assume value if H 0 proves true.

Step 3: Find out the value of P. P-value is the probability of data that is under observation.

Rise or increase in the P value = Pr(X ≥ x)

X = observed number of successes

P value = Pr(X ≤ x).

Step 4: Demonstrate the findings or outcomes in a descriptive detailed way.

• Sample proportion
• The direction of difference (either increases or decreases)

Perceived Problems With the Null Hypothesis

Variable or model selection and less information in some cases are the chief important issues that affect the testing of the null hypothesis. Statistical tests of the null hypothesis are reasonably not strong. There is randomization about significance. (Gill, 1999) The main issue with the testing of the null hypothesis is that they all are wrong or false on a ground basis.

There is another problem with the a-level . This is an ignored but also a well-known problem. The value of a-level is without a theoretical basis and thus there is randomization in conventional values, most commonly 0.q, 0.5, or 0.01. If a fixed value of a is used, it will result in the formation of two categories (significant and non-significant) The issue of a randomized rejection or non-rejection is also present when there is a practical matter which is the strong point of the evidence related to a scientific matter.

The P-value has the foremost importance in the testing of null hypothesis but as an inferential tool and for interpretation, it has a problem. The P-value is the probability of getting a test statistic at least as extreme as the observed one.

The main point about the definition is: Observed results are not based on a-value

Moreover, the evidence against the null hypothesis was overstated due to unobserved results. A-value has importance more than just being a statement. It is a precise statement about the evidence from the observed results or data. Similarly, researchers found that P-values are objectionable. They do not prefer null hypotheses in testing. It is also clear that the P-value is strictly dependent on the null hypothesis. It is computer-based statistics. In some precise experiments, the null hypothesis statistics and actual sampling distribution are closely related but this does not become possible in observational studies.

Some researchers pointed out that the P-value is depending on the sample size. If the true and exact difference is small, a null hypothesis even of a large sample may get rejected. This shows the difference between biological importance and statistical significance. (Killeen, 2005)

Another issue is the fix a-level, i.e., 0.1. On the basis, if a-level a null hypothesis of a large sample may get accepted or rejected. If the size of simple is infinity and the null hypothesis is proved true there are still chances of Type I error. That is the reason this approach or method is not considered consistent and reliable. There is also another problem that the exact information about the precision and size of the estimated effect cannot be known. The only solution is to state the size of the effect and its precision.

Null Hypothesis Examples

Here are some examples:

Example 1: Hypotheses with One Sample of One Categorical Variable

Among all the population of humans, almost 10% of people prefer to do their task with their left hand i.e. left-handed. Let suppose, a researcher in the Penn States says that the population of students at the College of Arts and Architecture is mostly left-handed as compared to the general population of humans in general public society. In this case, there is only a sample and there is a comparison among the known population values to the population proportion of sample value.

• Research Question: Do artists more expected to be left-handed as compared to the common population persons in society?
• Response Variable: Sorting the student into two categories. One category has left-handed persons and the other category have right-handed persons.
• Form Null Hypothesis: Arts and Architecture college students are no more predicted to be lefty as compared to the common population persons in society (Lefty students of Arts and Architecture college population is 10% or p= 0.10)

Example 2: Hypotheses with One Sample of One Measurement Variable

A generic brand of antihistamine Diphenhydramine making medicine in the form of a capsule, having a 50mg dose. The maker of the medicines is concerned that the machine has come out of calibration and is not making more capsules with the suitable and appropriate dose.

• Research Question: Does the statistical data recommended about the mean and average dosage of the population differ from 50mg?
• Response Variable: Chemical assay used to find the appropriate dosage of the active ingredient.
• Null Hypothesis: Usually, the 50mg dosage of capsules of this trade name (population average and means dosage =50 mg).

Example 3: Hypotheses with Two Samples of One Categorical Variable

Several people choose vegetarian meals on a daily basis. Typically, the researcher thought that females like vegetarian meals more than males.

• Research Question: Does the data recommend that females (women) prefer vegetarian meals more than males (men) regularly?
• Response Variable: Cataloguing the persons into vegetarian and non-vegetarian categories. Grouping Variable: Gender
• Null Hypothesis: Gender is not linked to those who like vegetarian meals. (Population percent of women who eat vegetarian meals regularly = population percent of men who eat vegetarian meals regularly or p women = p men).

Example 4: Hypotheses with Two Samples of One Measurement Variable

Nowadays obesity and being overweight is one of the major and dangerous health issues. Research is performed to confirm that a low carbohydrates diet leads to faster weight loss than a low-fat diet.

• Research Question: Does the given data recommend that usually, a low-carbohydrate diet helps in losing weight faster as compared to a low-fat diet?
• Response Variable: Weight loss (pounds)
• Explanatory Variable: Form of diet either low carbohydrate or low fat
• Null Hypothesis: There is no significant difference when comparing the mean loss of weight of people using a low carbohydrate diet to people using a diet having low fat. (population means loss of weight on a low carbohydrate diet = population means loss of weight on a diet containing low fat).

Example 5: Hypotheses about the relationship between Two Categorical Variables

A case-control study was performed. The study contains nonsmokers, stroke patients, and controls. The subjects are of the same occupation and age and the question was asked if someone at their home or close surrounding smokes?

• Research Question: Did second-hand smoke enhance the chances of stroke?
• Variables: There are 02 diverse categories of variables. (Controls and stroke patients) (whether the smoker lives in the same house). The chances of having a stroke will be increased if a person is living with a smoker.
• Null Hypothesis: There is no significant relationship between a passive smoker and stroke or brain attack. (odds ratio between stroke and the passive smoker is equal to 1).

Example 6: Hypotheses about the relationship between Two Measurement Variables

A financial expert observes that there is somehow a positive and effective relationship between the variation in stock rate price and the quantity of stock bought by non-management employees

• Response variable- Regular alteration in price
• Explanatory Variable- Stock bought by non-management employees
• Null Hypothesis: The association and relationship between the regular stock price alteration ($) and the daily stock-buying by non-management employees ($) = 0.

Example 7: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples

• Research Question: Is the relation between the bill paid in a restaurant and the tip given to the waiter, is linear? Is this relation different for dining and family restaurants?
• Explanatory Variable- total bill amount
• Response Variable- the amount of tip
• Null Hypothesis: The relationship and association between the total bill quantity at a family or dining restaurant and the tip, is the same.

Try to answer the quiz below to check what you have learned so far about the null hypothesis.

Choose the best answer. 

Send Your Results (Optional)

• Blackwelder, W. C. (1982). “Proving the null hypothesis” in clinical trials. Controlled Clinical Trials , 3(4), 345–353.
• Frick, R. W. (1995). Accepting the null hypothesis. Memory & Cognition, 23(1), 132–138.
• Gill, J. (1999). The insignificance of null hypothesis significance testing. Political Research Quarterly , 52(3), 647–674.
• Killeen, P. R. (2005). An alternative to null-hypothesis significance tests. Psychological Science, 16(5), 345–353.

©BiologyOnline.com. Content provided and moderated by Biology Online Editors.

Last updated on June 16th, 2022

You will also like...

Stems primarily provide plants structural support. This tutorial includes lectures on the external form of a woody twig ..

Community Patterns

Learn about community patterns and the ecological factors influencing these patterns. Revisit some of the ecosystems you..

Meiosis and Alternation of Generations

Plants are characterized by having alternation of generations in their life cycles. This tutorial is a review of plant m..

Running Water Freshwater Communities

This tutorial introduces flowing water communities, which bring new and dithering factors into the equation for possible..

Gene Action – Operon Hypothesis

Animal water regulation.

Animals adapt to their environment in aspects of anatomy, physiology, and behavior. This tutorial will help you understa..

Related Articles...

No related articles found

AP® Biology

The chi square test: ap® biology crash course.

• The Albert Team
• Last Updated On: March 7, 2024

The statistics section of the AP® Biology exam is without a doubt one of the most notoriously difficult sections. Biology students are comfortable with memorizing and understanding content, which is why this topic seems like the most difficult to master. In this article,  The Chi Square Test: AP® Biology Crash Course , we will teach you a system for how to perform the Chi Square test every time. We will begin by reviewing some topics that you must know about statistics before you can complete the Chi Square test. Next, we will simplify the equation by defining each of the Chi Square variables. We will then use a simple example as practice to make sure that we have learned every part of the equation. Finally, we will finish with reviewing a more difficult question that you could see on your AP® Biology exam .

Null and Alternative Hypotheses

As background information, first you need to understand that a scientist must create the null and alternative hypotheses prior to performing their experiment. If the dependent variable is not influenced by the independent variable , the null hypothesis will be accepted. If the dependent variable is influenced by the independent variable, the data should lead the scientist to reject the null hypothesis . The null and alternative hypotheses can be a difficult topic to describe. Let’s look at an example.

Consider an experiment about flipping a coin. The null hypothesis would be that you would observe the coin landing on heads fifty percent of the time and the coin landing on tails fifty percent of the time. The null hypothesis predicts that you will not see a change in your data due to the independent variable.

The alternative hypothesis for this experiment would be that you would not observe the coins landing on heads and tails an even number of times. You could choose to hypothesize you would see more heads, that you would see more tails, or that you would just see a different ratio than 1:1. Any of these hypotheses would be acceptable as alternative hypotheses.

Defining the Variables

Now we will go over the Chi-Square equation. One of the most difficult parts of learning statistics is the long and confusing equations. In order to master the Chi Square test, we will begin by defining the variables.

This is the Chi Square test equation. You must know how to use this equation for the AP® Bio exam. However, you will not need to memorize the equation; it will be provided to you on the AP® Biology Equations and Formulas sheet that you will receive at the beginning of your examination.

Now that you have seen the equation, let’s define each of the variables so that you can begin to understand it!

•   X 2  :The first variable, which looks like an x, is called chi squared. You can think of chi like x in algebra because it will be the variable that you will solve for during your statistical test. •   ∑ : This symbol is called sigma. Sigma is the symbol that is used to mean “sum” in statistics. In this case, this means that we will be adding everything that comes after the sigma together. •   O : This variable will be the observed data that you record during your experiment. This could be any quantitative data that is collected, such as: height, weight, number of times something occurs, etc. An example of this would be the recorded number of times that you get heads or tails in a coin-flipping experiment. •   E : This variable will be the expected data that you will determine before running your experiment. This will always be the data that you would expect to see if your independent variable does not impact your dependent variable. For example, in the case of coin flips, this would be 50 heads and 50 tails.

The equation should begin to make more sense now that the variables are defined.

Working out the Coin Flip

We have talked about the coin flip example and, now that we know the equation, we will solve the problem. Let’s pretend that we performed the coin flip experiment and got the following data:

Now we put these numbers into the equation:

Heads (55-50) 2 /50= .5

Tails (45-50) 2 /50= .5

Lastly, we add them together.

c 2 = .5+.5=1

Now that we have c 2 we must figure out what that means for our experiment! To do that, we must review one more concept.

Degrees of Freedom and Critical Values

Degrees of freedom is a term that statisticians use to determine what values a scientist must get for the data to be significantly different from the expected values. That may sound confusing, so let’s try and simplify it. In order for a scientist to say that the observed data is different from the expected data, there is a numerical threshold the scientist must reach, which is based on the number of outcomes and a chosen critical value.

Let’s return to our coin flipping example. When we are flipping the coin, there are two outcomes: heads and tails. To get degrees of freedom, we take the number of outcomes and subtract one; therefore, in this experiment, the degree of freedom is one. We then take that information and look at a table to determine our chi-square value:

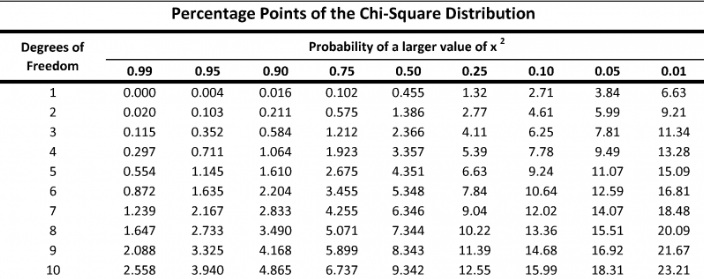
We will look at the column for one degree of freedom. Typically, scientists use a .05 critical value. A .05 critical value represents that there is a 95% chance that the difference between the data you expected to get and the data you observed is due to something other than chance. In this example, our value will be 3.84.

Coin Flip Results

In our coin flip experiment, Chi Square was 1. When we look at the table, we see that Chi Square must have been greater than 3.84 for us to say that the expected data was significantly different from the observed data. We did not reach that threshold. So, for this example, we will say that we failed to reject the null hypothesis.

The best way to get better at these statistical questions is to practice. Next, we will go through a question using the Chi Square Test that you could see on your AP® Bio exam.

AP® Biology Exam Question

This question was adapted from the 2013 AP® Biology exam.

In an investigation of fruit-fly behavior, a covered choice chamber is used to test whether the spatial distribution of flies is affected by the presence of a substance placed at one end of the chamber. To test the flies’ preference for glucose, 60 flies are introduced into the middle of the choice chamber at the insertion point. A ripe banana is placed at one end of the chamber, and an unripe banana is placed at the other end. The positions of flies are observed and recorded after 1 minute and after 10 minutes. Perform a Chi Square test on the data for the ten minute time point. Specify the null hypothesis and accept or reject it.

Okay, we will begin by identifying the null hypothesis . The null hypothesis would be that the flies would be evenly distributed across the three chambers (ripe, middle, and unripe).

Next, we will perform the Chi-Square test just like we did in the heads or tails experiment. Because there are three conditions, it may be helpful to use this set up to organize yourself:

Ok, so we have a Chi Square of 48.9. Our degrees of freedom are 3(ripe, middle, unripe)-1=2. Let’s look at that table above for a confidence variable of .05. You should get a value of 5.99. Our Chi Square value of 48.9 is much larger than 5.99 so in this case we are able to reject the null hypothesis. This means that the flies are not randomly assorting themselves, and the banana is influencing their behavior.

The Chi Square test is something that takes practice. Once you learn the system of solving these problems, you will be able to solve any Chi Square problem using the exact same method every time! In this article, we have reviewed the Chi Square test using two examples. If you are still interested in reviewing the bio-statistics that will be on your AP® Biology Exam, please check out our article The Dihybrid Cross Problem: AP® Biology Crash Course . Let us know how studying is going and if you have any questions!

Need help preparing for your AP® Biology exam?

Albert has hundreds of AP® Biology practice questions, free response, and full-length practice tests to try out.

Interested in a school license?​

Popular posts.

AP® Score Calculators

Simulate how different MCQ and FRQ scores translate into AP® scores

AP® Review Guides

The ultimate review guides for AP® subjects to help you plan and structure your prep.

Core Subject Review Guides

Review the most important topics in Physics and Algebra 1 .

SAT® Score Calculator

See how scores on each section impacts your overall SAT® score

ACT® Score Calculator

See how scores on each section impacts your overall ACT® score

Grammar Review Hub

Comprehensive review of grammar skills

AP® Posters

Download updated posters summarizing the main topics and structure for each AP® exam.

The Biology Corner

Biology Teaching Resources

Experimental Design

Students in most science classes start with an overview of scientific processes. For advanced students, I use this cheat sheet to remind them of the major features of the scientific method, such as a control group, dependent and independent variables .

AP Bio students are also introduced to the concept of the null and alternative hypotheses as well as how to statistically analyze data. Though this was made for AP Biology, you could make a copy of it (google docs) and then edit it to work other groups.

This guide can be used with introductory lessons like “ The Fortune Telling Fish ” where students can be asked to describe each feature of the design they used to determine what was causing the fish’s movements.

My anatomy and physiology classes and AP Bio classes do an investigation where they determine trends of lung capacity and physical features like height and sex.

This guide also clearly describes the difference between a hypothesis and a prediction. Many biology books describe them as being the same thing, but they are not. “ Teaching the Hypothesis ” is a great article on why the difference matters.

Shannan Muskopf