visual presentation of data by means of box plots

• The Future of Mass Spectrometry
• Separation Science - The State of The Art in Life Science Analysis
• PFAS Focus 2024: Water Analysis

• Publications
• Conferences

Visual Presentation of Data by Means of Box Plots

• Desire Luc Massart
• Johanna Smeyers-Verbeke

LCGC Europe

The authors explain how to construct box plots and how they can help you to learn more about your data.

Best of the Week: Advancements in MS, Bone Protein Analysis, and Technology Trends

Here is some of the most popular content posted on LCGC International this week.

LC–MS/MS for Quantifying Nitrosamines in Olmesartan Tablets

Mithibai College of Arts scientists recently used liquid chromatography-tandem mass spectrometry (LC–MS/MS) for detecting nitrosamines in blood pressure medication.

Technology Trends In Separation Science

Informative panel discussions featuring key opinion leaders from the separation science sector discussing the latest technology trends and developments in liquid chromatography, gas chromatography, sample preparation, and data handling.

GC/LC-Q-TOF/MS Method for Determining Pesticides in Traditional Chinese Medicine

Scientists recently developed new GC/LC-Q-TOF/MS-based method for determining pesticides in Angelica sinensis, a traditional Chinese medicine.

Mentorship in Science: Insights from FeMS Empowerment Award Winner Faith Johnson

LCGC International sat down with Faith Johnson of ECOLAB to discuss her career and work with the Females in Mass Spectrometry (FeMS) group.

Profiling Volatile Organic Compounds in Whisky with GC×GC–MS

Researchers from Austria, Greece, and Italy conducted a study to analyze volatile organic compounds (VOCs) present in Irish and Scotch whiskys using solid-phase microextraction (SPME) Arrow with comprehensive two-dimensional gas chromatography coupled to mass spectrometry (GC×GC–MS) to examine the organoleptic characteristics that influence the taste of spirits.

2 Commerce Drive Cranbury, NJ 08512

609-716-7777

• Help & FAQ

Visual Presentation of Data by Means of Box Plots

Desire Massart, Johanna Verbeke , Xavier Capron, K. Schlesier

• Analytical Chemistry and Pharmaceutical Technology
• Vrije Universiteit Brussel

Research output : Contribution to journal › Article

Bibliographical note

Visual Presentation of Data by Means of Box Plots. / Massart, Desire ; Verbeke, Johanna ; Capron, Xavier; Schlesier, K.

T1 - Visual Presentation of Data by Means of Box Plots

AU - Massart, Desire

AU - Verbeke, Johanna

AU - Capron, Xavier

AU - Schlesier, K.

N1 - LC-GC Europe, 18 (4), 2-5, 2005

M3 - Article

JO - LC-GC Europe

JF - LC-GC Europe

SN - 1471-6577

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 30 January 2014

Points of Significance

Visualizing samples with box plots

• Martin Krzywinski 1 &
• Naomi Altman 2  

Nature Methods volume  11 ,  pages 119–120 ( 2014 ) Cite this article

204k Accesses

387 Citations

78 Altmetric

Metrics details

• Research data
• Statistical methods

Use box plots to illustrate the spread and differences of samples.

You have full access to this article via your institution.

Visualization methods enhance our understanding of sample data and help us make comparisons across samples. Box plots are a simple but powerful graphing tool that can be used in place of histograms to address both goals. Whereas histograms require a sample size of at least 30 to be useful, box plots require a sample size of only 5, provide more detail in the tails of the distribution and are more readily compared across three or more samples. Several enhancements to the basic box plot can render it even more informative.

Box plots characterize a sample using the 25th, 50th and 75th percentiles—also known as the lower quartile (Q1), median ( m or Q2) and upper quartile (Q3)—and the interquartile range (IQR = Q3 − Q1), which covers the central 50% of the data. Quartiles are insensitive to outliers and preserve information about the center and spread. Consequently, they are preferred over the mean and s.d. for population distributions that are asymmetric or irregularly shaped and for samples with extreme outliers. In such cases these measures may be difficult to intuitively interpret: the mean may be far from the bulk of the data, and conventional rules for interpreting the s.d. will likely not apply.

The core element that gives the box plot its name is a box whose length is the IQR and whose width is arbitrary ( Fig. 1 ). A line inside the box shows the median, which is not necessarily central. The plot may be oriented vertically or horizontally—we use here (with one exception) horizontal boxes to maintain consistent orientation with corresponding sample distributions. Whiskers are conventionally extended to the most extreme data point that is no more than 1.5 × IQR from the edge of the box (Tukey style) or all the way to minimum and maximum of the data values (Spear style). The use of quartiles for box plots is a well-established convention: boxes or whiskers should never be used to show the mean, s.d. or s.e.m. As with the division of the box by the median, the whiskers are not necessarily symmetrical ( Fig. 1b ). The 1.5 multiplier corresponds to approximately ±2.7σ (where σ is s.d.) and 99.3% coverage of the data for a normal distribution. Outliers beyond the whiskers may be individually plotted. Box plot construction requires a sample of at least n = 5 (preferably larger), although some software does not check for this. For n < 5 we recommend showing the individual data points.

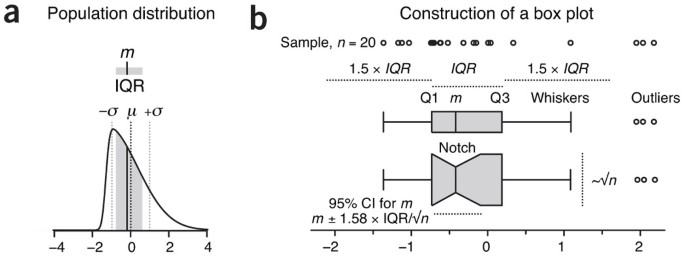
( a ) The median ( m = −0.19, solid vertical line) and interquartile range (IQR = 1.38, gray shading) are ideal for characterizing asymmetric or irregularly shaped distributions. A skewed normal distribution is shown with mean μ = 0 (dark dotted line) and s.d. σ = 1 (light dotted lines). ( b ) Box plots for an n = 20 sample from a . The box bounds the IQR divided by the median, and Tukey-style whiskers extend to a maximum of 1.5 × IQR beyond the box. The box width may be scaled by √ n , and a notch may be added approximating a 95% confidence interval (CI) for the median. Open circles are sample data points. Dotted lines indicate the lengths or widths of annotated features.

Sample size differences can be assessed by scaling the box plot width in proportion to √ n ( Fig. 1b ), the factor by which the precision of the sample's estimate of population statistics improves as sample size is increased.

To assist in judging differences between sample medians, a notch ( Fig. 1b ) can be used to show the 95% confidence interval (CI) for the median, given by m ± 1.58 × IQR/√ n (ref. 1 ). This is an approximation based on the normal distribution and is accurate in large samples for other distributions. If you suspect the population distribution is not close to normal and your sample size is small, avoid interpreting the interval analytically in the way we have described for CI error bars 2 . In general, when notches do not overlap, the medians can be judged to differ significantly, but overlap does not rule out a significant difference. For small samples the notch may span a larger interval than the box ( Fig. 2 ).

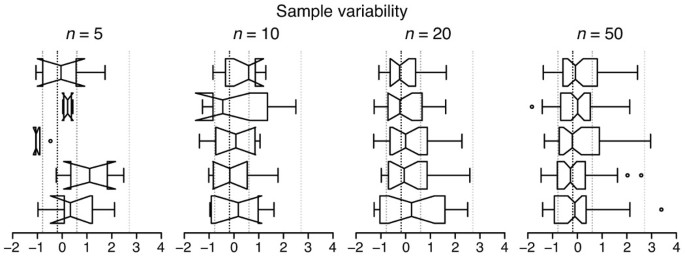
Tukey-style box plots for five samples with sample size n = 5, 10, 20 and 50 drawn from the distribution in Figure 1a are shown; notch width is as in Figure 1b . Vertical dotted lines show Q1 (−0.78), median (−0.19), Q3 (0.60) and Q3 + 1.5 × IQR (2.67) values for the distribution.

The exact position of box boundaries will be software dependent. First, there is no universally agreed-upon method to calculate quartile values, which may be based on simple averaging or linear interpolation. Second, some applications, such as R, use hinges instead of quartiles for box boundaries. The lower and upper hinges are the median of the lower and upper half of the data, respectively, including the median if it is part of the data. Boxes based on hinges will be slightly different in some circumstances than those based on quartiles.

Aspects of the box plot such as width, whisker position, notch size and outlier display are subject to tuning; it is therefore important to clearly label how your box plot was constructed. Fewer than 20% of box plot figures in 2013 Nature Methods papers specified both sample size and whisker type in their legends—we encourage authors to be more specific.

The box plot is based on sample statistics, which are estimates of the corresponding population values. Sample variability will be reflected in the variation of all aspects of the box plot ( Fig. 2 ). Modest sample sizes ( n = 5–10) from the same population can yield very different box plots whose notches are likely to extend beyond the IQR. Even for large samples ( n = 50), whisker positions can vary greatly. We recommend always indicating the sample size and avoiding notches unless they fall entirely within the IQR.

Although the mean and s.d. can always be calculated for any sample, they do not intuitively communicate the distribution of values ( Fig. 3 ). Highly skewed distributions appear in box plot form with a markedly shorter whisker-and-box region and an absence of outliers on the side opposite the skew. Keep in mind that for small sample sizes, which do not necessarily represent the distribution well, these features may appear by chance.

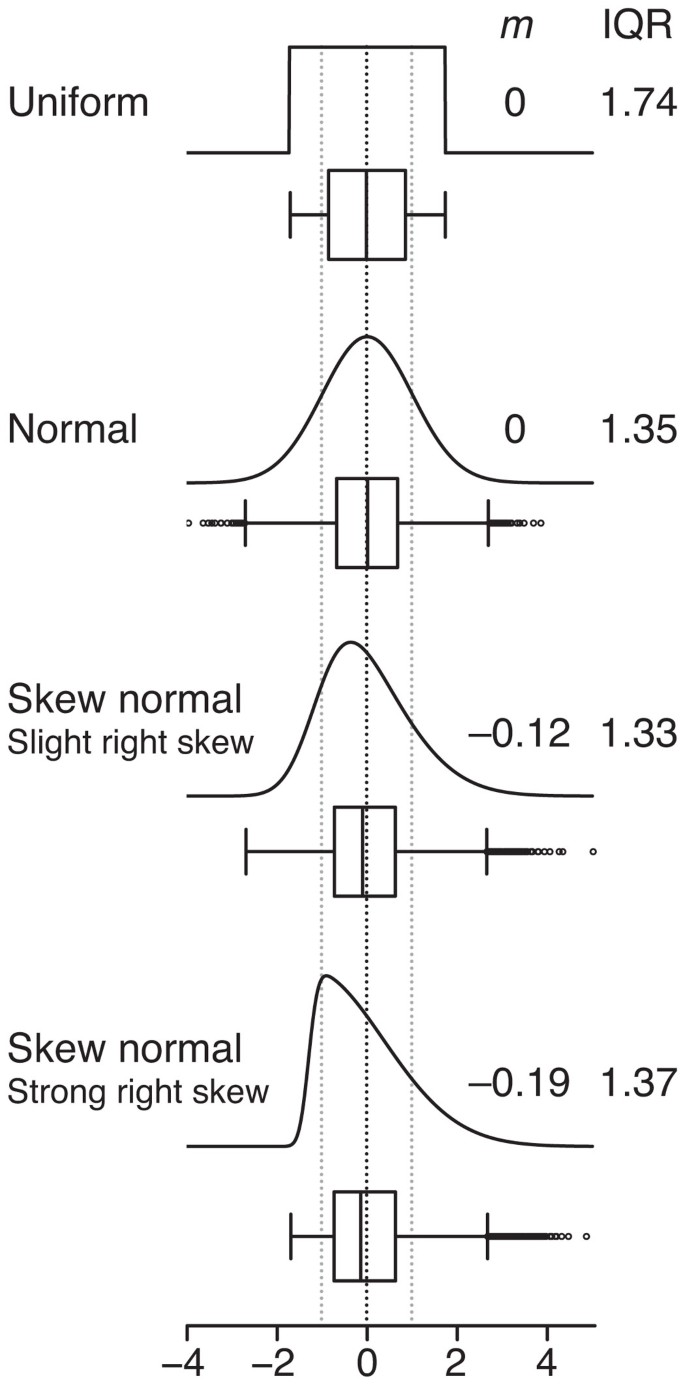
Four distributions with the same mean ( μ = 0, dark dotted line) and s.d. (σ = 1, light dotted lines) but significantly different medians ( m ) and IQRs are shown with corresponding Tukey-style box plots for n = 10,000 samples.

We strongly discourage using bar plots with error bars ( Fig. 4a ), which are best used for counts or proportions 3 . These charts continue to be prevalent (we counted 100 figures that used them in 2013 Nature Methods papers, compared to only 20 that used box plots). They typically show only one arm of the error bar, making overlap comparisons difficult. More importantly, the bar itself encourages the perception that the mean is related to its height rather than the position of its top. As a result, the choice of baseline can interfere with assessing relative sizes of means and their error bars. The addition of axis breaks and log scaling makes visual comparisons even more difficult.

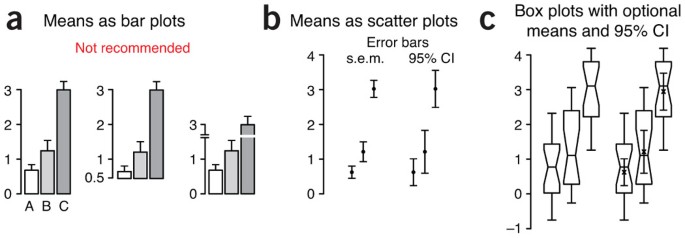
Data are shown for three n = 20 samples from normal distributions with s.d. σ = 1 and mean μ = 1 (A,B) or 3 (C). ( a ) Showing sample mean and s.e.m. using bar plots is not recommended. Note how the change of baseline or cutting the y axis affects the comparative heights of the bars. ( b ) When sample size is sufficiently large ( n > 3), scatter plots with s.e.m. or 95% confidence interval (CI) error bars are suitable for comparing central tendency. ( c ) Box plots may be combined with sample mean and 95% CI error bars to communicate more information about samples in roughly the same amount of space.

The traditional mean-and-error scatter plot with s.e.m. or 95% CI error bars ( Fig. 4b ) can be incorporated into box plots ( Fig. 4c ), thus combining details about the sample with an estimate of the population mean. For small samples, the s.e.m. bar may extend beyond the box. If data are normally distributed, >95% of s.e.m. bars will be within the IQR for n ≥ 14. For 95% CI bars, the cutoff is n ≥ 28.

Because they are based on statistics that do not require us to assume anything about the shape of the distribution, box plots robustly provide more information about samples than conventional error bars. We encourage their wider use and direct the reader to http://boxplot.tyerslab.com/ (ref. 4 ), a convenient online tool to create box plots that implements all the options described here.

McGill, R., Tukey, J.W & Larsen, W.A. Am. Stat. 32 , 12–16 (1978).

Google Scholar  

Krzywinski, M. & Altman, N. Nat. Methods 10 , 921–922 (2013).

Article   CAS   Google Scholar  

Streit, M. & Gehlenborg, N. Nat. Methods 11 , 117 (2014).

Spitzer, M. et al. Nat. Methods 11 , 121–122 (2014).

Download references

Author information

Authors and affiliations.

Martin Krzywinski is a staff scientist at Canada's Michael Smith Genome Sciences Centre.,

Martin Krzywinski

Naomi Altman is a Professor of Statistics at The Pennsylvania State University.,

Naomi Altman

You can also search for this author in PubMed   Google Scholar

Ethics declarations

Competing interests.

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Krzywinski, M., Altman, N. Visualizing samples with box plots. Nat Methods 11 , 119–120 (2014). https://doi.org/10.1038/nmeth.2813

Download citation

Published : 30 January 2014

Issue Date : February 2014

DOI : https://doi.org/10.1038/nmeth.2813

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Cage escape governs photoredox reaction rates and quantum yields.

• Oliver S. Wenger

Nature Chemistry (2024)

A novel ionospheric TEC mapping function with azimuth parameters and its application to the Chinese region

• Xingliang Huo
• Yuanliang Long
• Weihong Sun

Journal of Geodesy (2024)

International bureaucrats’ attitudes toward global climate adaptation

• Lisa Dellmuth

npj Climate Action (2023)

The Microbiota of a Mite Prey-Predator System on Different Host Plants Are Characterized by Dysbiosis and Potential Functional Redundancy

• Bruna Laís Merlin
• Gilberto J. Moraes
• Fernando L. Cônsoli

Microbial Ecology (2023)

An API for dynamic estimation of reference intervals for functional abundances of gut microbiota

• Leman Binokay
• Yavuz Oktay
• Gökhan Karakülah

Biologia (2023)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Box Plot Explained: Interpretation, Examples, & Comparison

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

In descriptive statistics, a box plot or boxplot (also known as a box and whisker plot) is a type of chart often used in explanatory data analysis. Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages.

Box plots show the five-number summary of a set of data: including the minimum score, first (lower) quartile, median, third (upper) quartile, and maximum score.

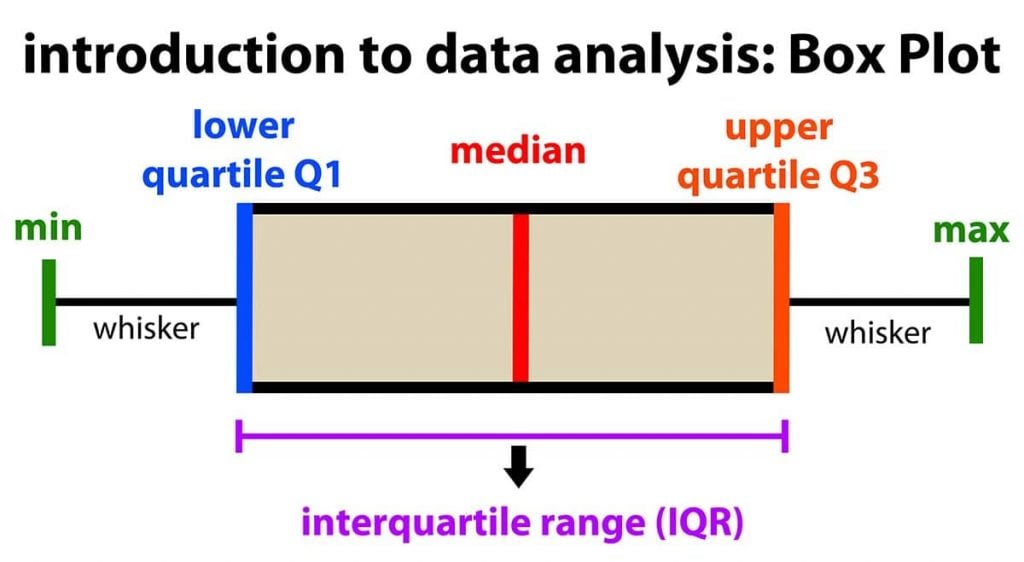
Definitions

Minimum score.

The lowest score, excluding outliers (shown at the end of the left whisker).

Lower Quartile

Twenty-five percent of scores fall below the lower quartile value (also known as the first quartile).

The median marks the mid-point of the data and is shown by the line that divides the box into two parts (sometimes known as the second quartile). Half the scores are greater than or equal to this value, and half are less.

Upper Quartile

Seventy-five percent of the scores fall below the upper quartile value (also known as the third quartile). Thus, 25% of data are above this value.

Maximum Score

The highest score, excluding outliers (shown at the end of the right whisker).

The upper and lower whiskers represent scores outside the middle 50% (i.e., the lower 25% of scores and the upper 25% of scores).

The Interquartile Range (or IQR)

The box plot shows the middle 50% of scores (i.e., the range between the 25th and 75th percentile).

Why are box plots useful?

Box plots divide the data into sections containing approximately 25% of the data in that set.

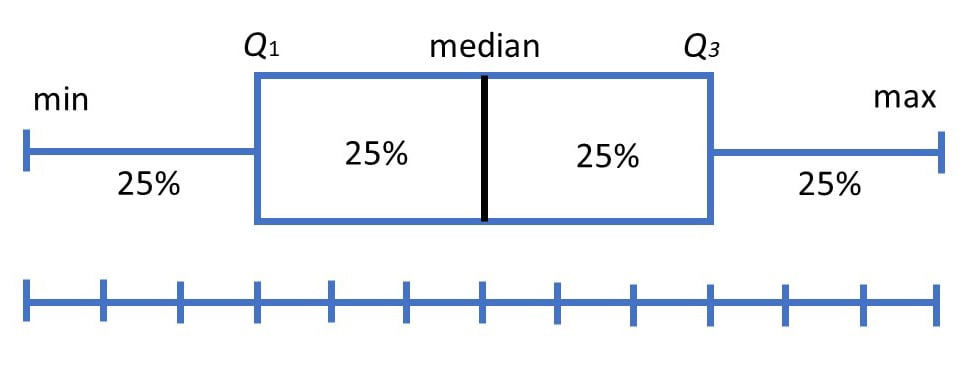
Box plots are useful as they provide a visual summary of the data enabling researchers to quickly identify mean values, the dispersion of the data set, and signs of skewness.

Note that the image above represents data that has a perfect normal distribution , and most box plots will not conform to this symmetry (where each quartile is the same length).

Box plots are useful as they show the average score of a data set

The median is the average value from a set of data and is shown by the line that divides the box into two parts. Half the scores are greater than or equal to this value, and half are less.

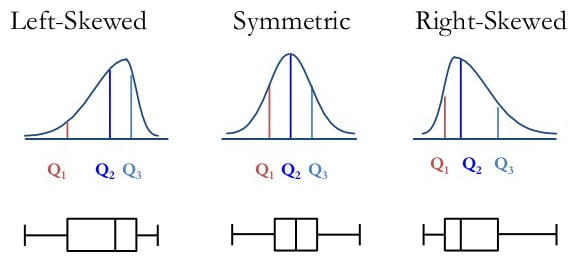
Box plots are useful as they show the skewness of a data set

The box plot shape will show if a statistical data set is normally distributed or skewed.

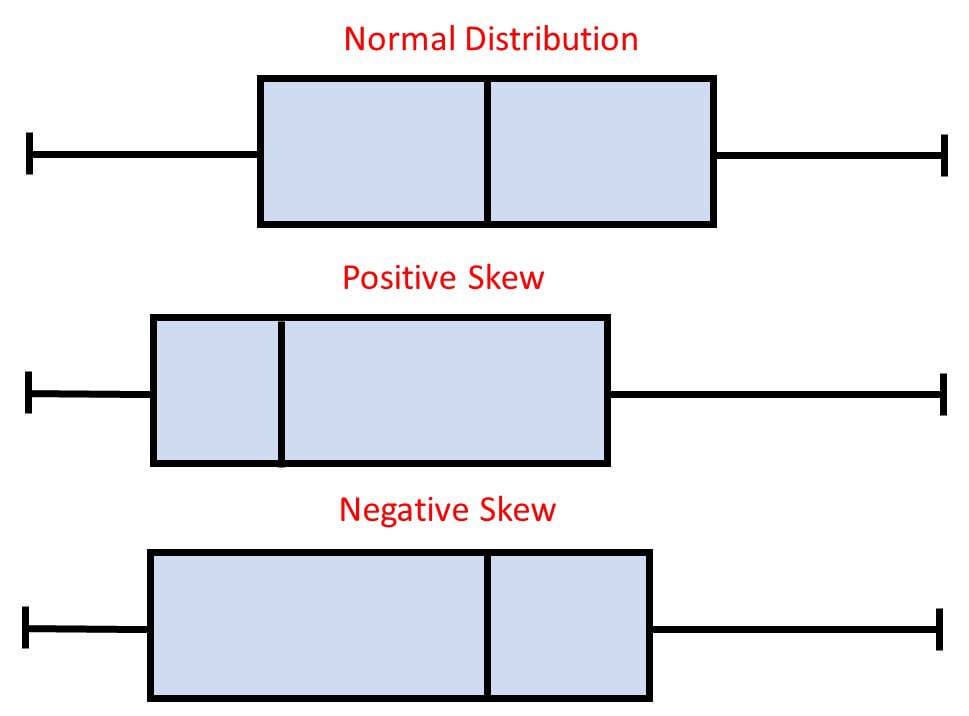
When the median is in the middle of the box, and the whiskers are about the same on both sides of the box, then the distribution is symmetric.

When the median is closer to the bottom of the box, and if the whisker is shorter on the lower end of the box, then the distribution is positively skewed (skewed right).

When the median is closer to the top of the box, and if the whisker is shorter on the upper end of the box, then the distribution is negatively skewed (skewed left).

Box plots are useful as they show the dispersion of a data set

In statistics, dispersion (also called variability, scatter, or spread) is the extent to which a distribution is stretched or squeezed.

The smallest and largest values are found at the end of the ‘whiskers’ and are useful for providing a visual indicator regarding the spread of scores (e.g., the range).

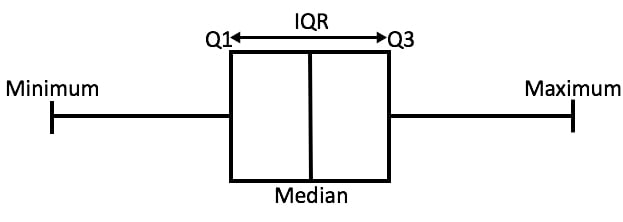
The interquartile range (IQR) is the box plot showing the middle 50% of scores and can be calculated by subtracting the lower quartile from the upper quartile (e.g., Q3−Q1).

Box plots are useful as they show outliers within a data set

An outlier is an observation that is numerically distant from the rest of the data.

When reviewing a box plot, an outlier is defined as a data point that is located outside the whiskers of the box plot.

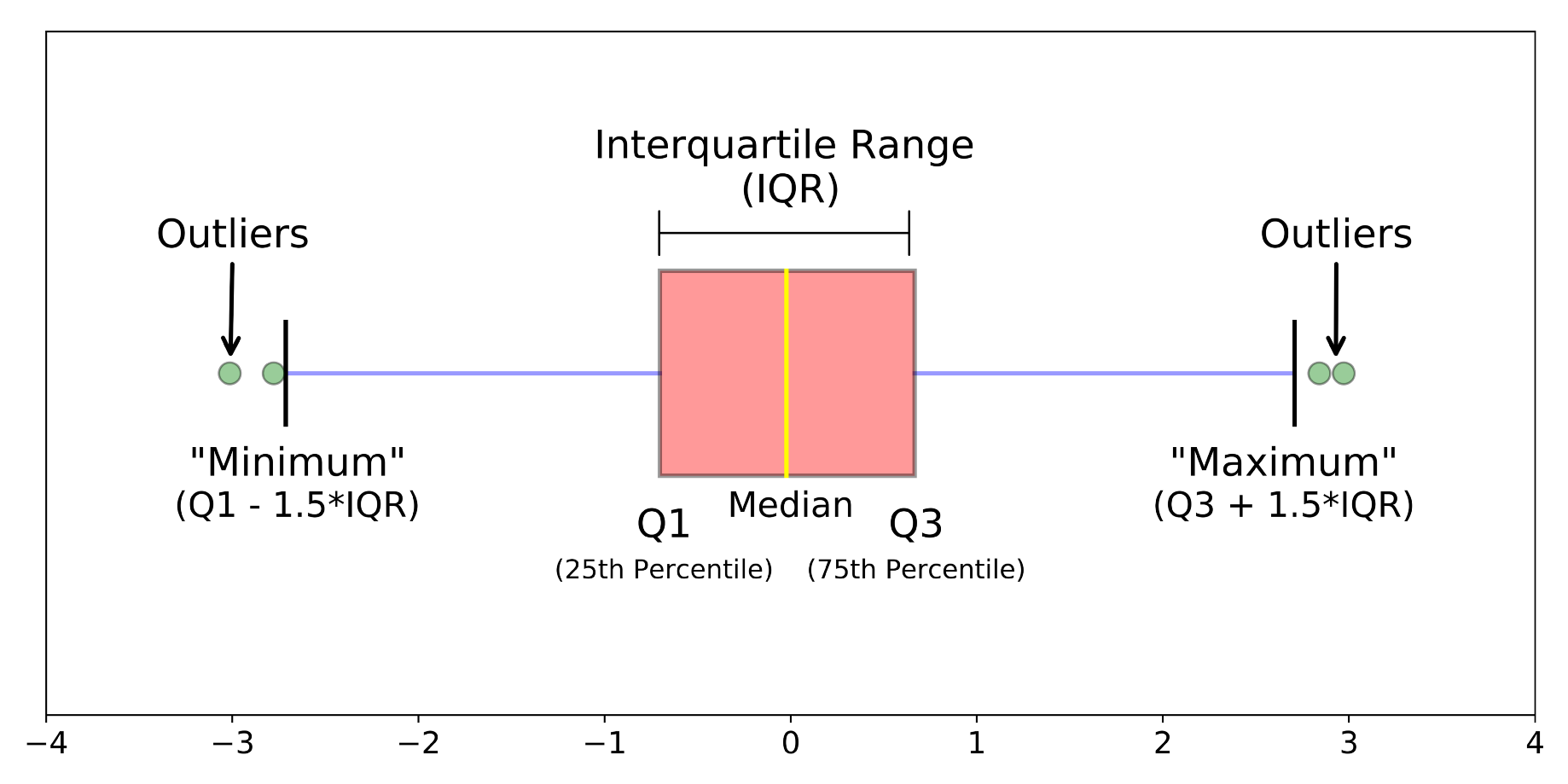
Source: https://towardsdatascience.com/understanding-boxplots-5e2df7bcbd51

For example, outside 1.5 times the interquartile range above the upper quartile and below the lower quartile (Q1 – 1.5 * IQR or Q3 + 1.5 * IQR).

How to compare box plots

Box plots are a useful way to visualize differences among different samples or groups. They manage to provide a lot of statistical information, including — medians, ranges, and outliers.

Step 1: Compare the medians of box plots

Compare the respective medians of each box plot. If the median line of a box plot lies outside of the box of a comparison box plot, then there is likely to be a difference between the two groups.

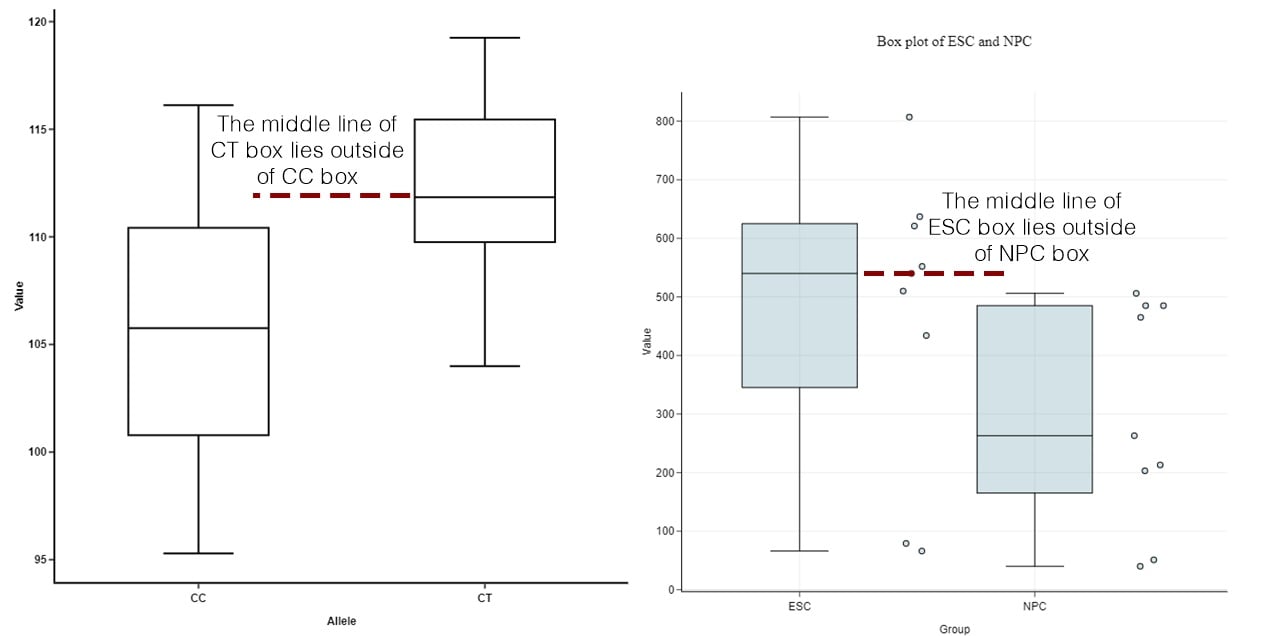
Source: https://blog.bioturing.com/2018/05/22/how-to-compare-box-plots/

Step 2: Compare the interquartile ranges and whiskers of box plots

Compare the interquartile ranges (that is, the box lengths) to examine how the data is dispersed between each sample. The longer the box, the more dispersed the data. The smaller, the less dispersed the data.

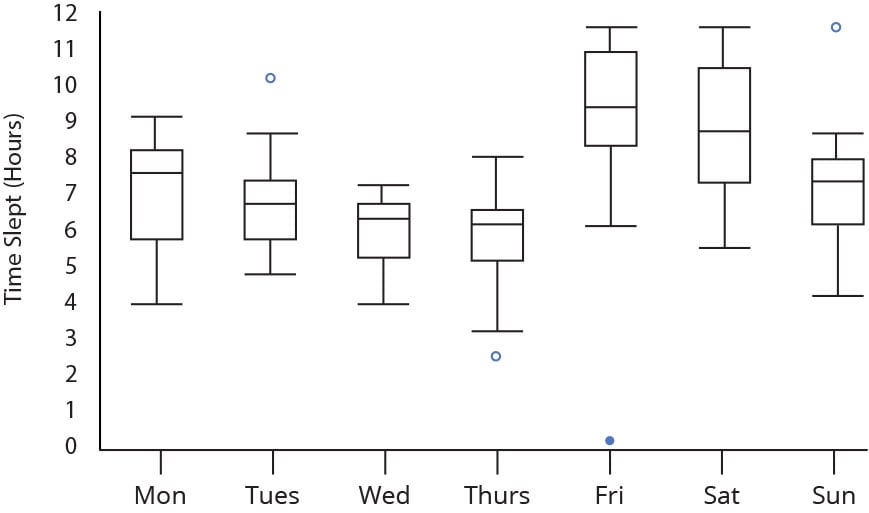
Next, look at the overall spread as shown by the extreme values at the end of two whiskers. This shows the range of scores (another type of dispersion). Larger ranges indicate wider distribution, that is, more scattered data.

Step 3: Look for potential outliers (see the above image)

Step 4: look for signs of skewness.

If the data do not appear to be symmetric, does each sample show the same kind of asymmetry?

What Is a Box Plot and When to Use It

Let’s wrap up this trilogy in the smoothest way possible. By now, you’ve had ample opportunity to read about creating a Bell (Gaussian) Curve , and you’ve read why Pareto Curves are better , more accurate depictions of a statistical view on a subset of data. Let’s finally discuss the built-in visualization that we already have in our Chart Library in Chartio, that you can create.

In this tutorial, I will go through step by step instructions on how to create a box plot visualization, explain the arithmetic of each data point outlined in a box plot, and we will mention a few perfect use cases for a box plot.

What is a Box Plot?

A Box Plot is the visual representation of the statistical five number summary of a given data set.

A Five Number Summary includes:

• First Quartile
• Median (Second Quartile)
• Third Quartile

Mathematician John Tukey first introduced the “Box and Whisker Plot” in 1969 as a visual diagram of the “Five Number Summary” of any given data set. As Hadley Wickham describes, “Box plots use robust summary statistics that are always located at actual data points, are quickly computable (originally by hand), and have no tuning parameters. They are particularly useful for comparing distributions across groups.” Source .

Box and whisker plots have been used steadily since their introduction in 1969 and are varied in both their potential visualizations as well as use cases across many disciplines in statistics and data analysis.

The Chartio version of the Box Plot is close to the original definition and presentation, and is used to take a subset of data and quickly and visually show the five number summary of that data set. Also, in Chartio’s version, a tool tip is provided that shows all of the data points summarized in the visualization.

How to create a box plot

We will demonstrate the creation of a Box Plot so we can compare it to the Bell Curve you created while following the first tutorial .

The goal here is to show how the distribution will be distributed using our visualization built for you as it compares to the more complex to create and less indicative of an actual population Bell Curve.

1.) We need to create the same query we did in that tutorial, which in SQL syntax is seen here:

As seen previously we need to drag the Cost to the dimensions box to show each customer payment amount to our company in one chart, and that is it. As opposed to how we needed to show the Customer as well to determine the distribution in the Bell Curve we only need each amount in the dimensions box.

2.) Then we need to click on the box plot icon in the Chart Library below the Chart Preview Screen.

As promised, this is far less complicated. Even if you want to add some more dimensionality to it, and see how these amounts are brought in by month, all you would need to do is to add the created date, bucketed by month, to the dimensions box and re-run your query.

What’s in the Box?

Now, that we know how to create a Box Plot we will cover the five number summary, to explain the numbers that are in the tool tip and make up the box plot itself.

First, the Five Number Summary is the Sample Minimum, the lower quartile or first quartile, the median, the upper quartile or third quartile and the sample maximum. Traditionally the box plot should be the Five Number Summary and in a very basic number set Chartio will assign the values in the box plot to the Five Number Summary. This is not the literal number for each of those five numbers, instead it is the closest number in the data set to those numbers.

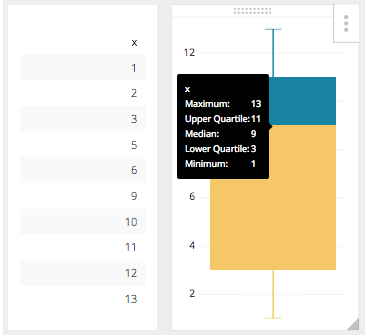
For example in the number set where x = 1, 2, 3, 5, 6, 9, 10, 11, 12, 13

The literal Five Number Summary would be this:

However, the true Five Number Summary would be the closest values within our dataset to the numbers calculated in the Five Number Summary so our result set will actually be this:

You can see this presented in Chartio here, with the tooltip visible:

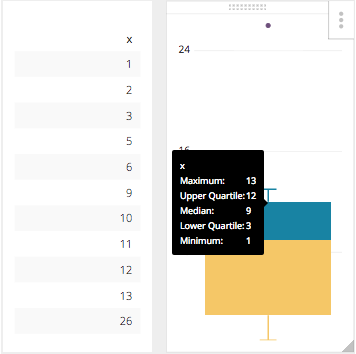
That is pretty straight forward, but it can get complicated when the dataset it a much larger set of numbers, or if the data set range is much larger. What happens then is there is an adjustment to the Five Number Range, and that is to find the upper and lower end of the whiskers. This new limit is calculated using the Interquartile Range or IQR. This number is the distance between the Upper and Lower Quartile, or in our example it would be 8. That being said the new upper whisker is the first number that is less than the Upper Quartile (3Q) + 1.5 IQR, in our case it is still 13. With this new facet in our equation the highest value of 26 which is outside 3Q + 1.5 IQR is now considered the outlier which Chartio will show as an individual plot point.

The Box Plot is a very useful tool when showing a statistical distribution and is much easier to build in Chartio because we have already included this as an item in our Chart Library.

similar articles

A complete guide to funnel charts.

Funnel charts are specialized charts for showing the flow of users through a process. Learn how to best use this chart type by reading this article.

A Complete Guide to Violin Plots

Violin plots are used to compare the distribution of data between groups. Learn how violin plots are constructed and how to use them in this article.

A Complete Guide to Heatmaps

Heatmaps take the form of a grid of colored squares, where colors correspond with cell value. This article will show you how to best use this chart type.